题目内容
16．要使代数式$\frac{\sqrt{x+2}}{x-3}$有意义，则x的取值范围是-2≤x＜3且x＞3．分析 根据二次根式的性质和分式的意义，被开方数大于或等于0，分母不等于0，可以求出x的范围．
解答 解：由代数式$\frac{\sqrt{x+2}}{x-3}$有意义，得
$\left\{\begin{array}{l}{x+2≥0}\\{x-3≠0}\end{array}\right.$．
解得-2≤x＜3且x＞3，
故答案为：-2≤x＜3且x＞3．
点评 本题考查了二次根式有意义的条件，函数自变量的范围一般从三个方面考虑：当函数表达式是整式时，自变量可取全体实数；当函数表达式是分式时，考虑分式的分母不能为0；当函数表达式是二次根式时，被开方数非负．
练习册系列答案
相关题目
已知：如图，∠1=∠2，∠E=∠F，则AB∥CD吗？说明理由．
5．我们定义一种变换§：对于一个由5个数组成的数列S1，将其中的每个数换成该数在S1中出现的次数，可得到一个新数列S2．例如：当数列S1是 （4，2，3，4，2）时，经过变换§可得到的新数列S2是（2，2，1，2，2）．若数列S1可以由任意5个数组成，则下列的数列可作为S2的是（ ）
| A． | （1，2，1，2，2） | B． | （2，2，2，3，3） | C． | （1，1，2，2，3） | D． | （1，2，1，1，2） |
11．某公司招聘一名公关人员，对甲、乙、丙、丁四位候选人进行了面试和笔试，他们的成绩如下表所示：
如果公司认为，作为公关人员面试的成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权．公司将录取（ ）
| 候选人 | 甲 | 乙 | 丙 | 丁 | |
| 测试成绩 （百分制） | 面试 | 86 | 92 | 90 | 83 |
| 笔试 | 90 | 83 | 83 | 92 | |
| A． | 甲 | B． | 乙 | C． | 丙 | D． | 丁 |
的运算结果正确的是（ ）
B. 
C. 
D. a+b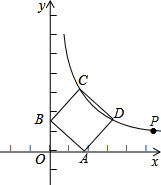
如图，点P（$\sqrt{3}$+1，$\sqrt{3}$-1）在双曲线y=$\frac{k}{x}$（x＞0）上．