题目内容
19．把前2015个数1，2，3，…，2015的每一个数的前面任意填上“+”号或“-”号，然后将它们相加，则所得之结果为（ ）| A． | 正数 | B． | 奇数 | ||
| C． | 偶数 | D． | 有时为奇数；有时为偶数 |
分析 把1+2+…+2014+2015求出之和，根据奇偶性判断即可得到结果．
解答 解：1+2+3+…+2015=$\frac{（1+2015）×2015}{2}$=1008×2015，
原和为偶数，只要一个数改变它的符合，和为这个数的2倍，一加一减，奇偶性不变，
故选C
点评 此题考查了有理数的加减混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
天天练口算系列答案
相关题目
9．
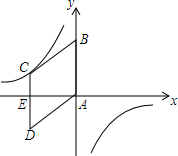如图，在平面直角坐标系中，菱形ABCD的顶点A与原点O重合，点B在y轴的正半轴上，点C在反比例函数y=$\frac{k}{x}$的图象上，点D的坐标为（-4，-3），CD与x轴交于点E，求k的值．
如图，在平面直角坐标系中，菱形ABCD的顶点A与原点O重合，点B在y轴的正半轴上，点C在反比例函数y=$\frac{k}{x}$的图象上，点D的坐标为（-4，-3），CD与x轴交于点E，求k的值． 
如图，直线y=k（x-2）+k-1与x轴、y轴分别交于B、C两点，且$\frac{OB}{OC}$=$\frac{1}{2}$．
如图，△ABC中，BD平分∠ABC，BC的中垂线交BC于点E，交BD于点F，连接CF．若∠A=60°，∠ABD=24°，则∠ACF=48°．
14．在如图所示的三个函数图象中，有两个函数图象能近似地刻画如下a，b两个情境：
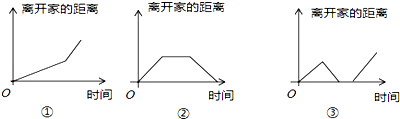
情境a：小芳离开家不久，发现把作业本忘在家里，于是返回了家里找到了作业本再去学校；
情境b：小芳从家出发，走了一段路程后，为了赶时间，以更快的速度前进．则情境a，b所对应的函数图象分别是（ ）
情境a：小芳离开家不久，发现把作业本忘在家里，于是返回了家里找到了作业本再去学校；
情境b：小芳从家出发，走了一段路程后，为了赶时间，以更快的速度前进．则情境a，b所对应的函数图象分别是（ ）
| A． | ③、② | B． | ②、③ | C． | ①、③ | D． | ③、① |
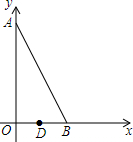如图，在平面直角坐标系xOy中，点A在y轴上，点B在x轴上，∠ABO=60°，若点D（1，0）且BD=2OD．把△ABO绕着点D逆时针旋转m°（0＜m＜180）后，点B恰好落在初始Rt△ABO的边上，此时的点B记为B′，则点B′的坐标为（2，$\sqrt{3}$）或（0，$\sqrt{3}$）．
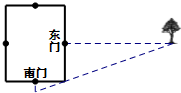《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．其中卷第九勾股，主要讲述了以测量问题为中心的直角三角形三边互求的关系．其中记载：“今有邑，东西七里，南北九里，各中开门，出东门一十五里有木，问：出南门几何步而见木？”
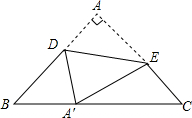如图，已知△ABC中，∠A=90°，AB=AC，AB=3+3$\sqrt{2}$，点D在AB上，点E在AC上，△ADE沿DE折叠后点A恰好落在BC上的A′点，且DA′⊥BC．则A′B的长是3．
17．下列根式是最简二次根式的是（ ）
| A． | $\sqrt{{m^2}-{n^2}}$ | B． | $\sqrt{\frac{1}{2}}$ | C． | $\sqrt{x^5}$ | D． | $\sqrt{8}$ |