Question

4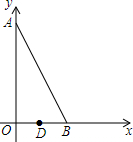．如图，在平面直角坐标系xOy中，点A在y轴上，点B在x轴上，∠ABO=60°，若点D（1，0）且BD=2OD．把△ABO绕着点D逆时针旋转m°（0＜m＜180）后，点B恰好落在初始Rt△ABO的边上，此时的点B记为B′，则点B′的坐标为（2，$\sqrt{3}$）或（0，$\sqrt{3}$）．

Answer 1

分析 分类讨论：当点B恰好落在AB上，如图1，根据旋转的性质得DB=DB′=2，易得△DBB′为等边三角形，作B′E⊥DB于E，如图1，根据等边三角形的性质得DE=BE=$\frac{1}{2}$BD=1，B′E=$\sqrt{3}$DE=$\sqrt{3}$，则B′（2，$\sqrt{3}$）；当点B恰好落在OA上，如图1，根据旋转的性质得DB=DB′=2，利用勾股定理计算出OB′=$\sqrt{3}$，则B′（0，$\sqrt{3}$），于是得到B′点的坐标为（2，$\sqrt{3}$）或（0，$\sqrt{3}$）．

解答 解：∵点D（1，0）且BD=2OD，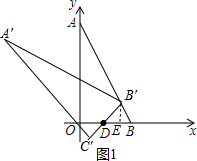
∴BD=2，
当把△ABO绕着点D逆时针旋转m°（0＜m＜180）后得到△A′B′C′，点B恰好落在AB上，如图1，
∴DB=DB′，
而∠ABO=60°，
∴△DBB′为等边三角形，
作B′E⊥DB于E，如图1，
∴DE=BE=$\frac{1}{2}$BD=1，B′E=$\sqrt{3}$DE=$\sqrt{3}$，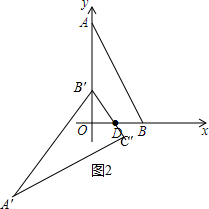
∴B′（2，$\sqrt{3}$）；
当把△ABO绕着点D逆时针旋转m°（0＜m＜180）后得到△A′B′C′，点B恰好落在OA上，如图1，
∴DB=DB′=2，
∴OB′=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$，
∴B′（0，$\sqrt{3}$）．
故答案为（2，$\sqrt{3}$）或（0，$\sqrt{3}$）．

点评 本题考查了坐标与图形变化-旋转：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30°，45°，60°，90°，180°．解决本题的关键是分类画出满足条件的几何图形．