题目内容
16.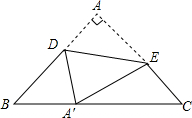 如图,已知△ABC中,∠A=90°,AB=AC,AB=3+3$\sqrt{2}$,点D在AB上,点E在AC上,△ADE沿DE折叠后点A恰好落在BC上的A′点,且DA′⊥BC.则A′B的长是3.
如图,已知△ABC中,∠A=90°,AB=AC,AB=3+3$\sqrt{2}$,点D在AB上,点E在AC上,△ADE沿DE折叠后点A恰好落在BC上的A′点,且DA′⊥BC.则A′B的长是3.
分析 设A′B=x,根据等腰直角三角形的性质可得∠B=45°,根据直角三角形两锐角互余求出∠BDA′=45°,再根据直角三角形的性质得到BD=$\sqrt{2}$A′B,然后利用勾股定理列式表示出A′D,再根据翻折的性质可得AD=A′D,最后根据AB=BD+AD列出方程求解即可.
解答 解:设A′B=x,
∵△ABC是等腰直角三角形,
∴∠B=45°,
∵DA′⊥BC,
∴∠BDA′=90°-45°=45°,
∴BD=$\sqrt{2}$A′B=$\sqrt{2}$x,
∴A′D=A′B=x,
由翻折的性质得,AD=A′D=x,
所以,AB=BD+AD=$\sqrt{2}$x+x=3+3$\sqrt{2}$,解得x=3,
即A′B=3.
故答案为:3.
点评 本题考查了翻折变换的性质,等边三角形的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,勾股定理,熟记各性质并用A′B表示出相关的线段是解题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
19.把前2015个数1,2,3,…,2015的每一个数的前面任意填上“+”号或“-”号,然后将它们相加,则所得之结果为( )
| A. | 正数 | B. | 奇数 | ||
| C. | 偶数 | D. | 有时为奇数;有时为偶数 |
5.估计$\sqrt{8}+1$的值在( )
| A. | 2到3之间 | B. | 3到4之间 | C. | 4到5之间 | D. | 5到6之间 |
 如图所示,已知四边形AOBC的各个顶点坐标分别为A(2,10),O(0,0),B(8,0),C(7,8),这个四边形的面积.
如图所示,已知四边形AOBC的各个顶点坐标分别为A(2,10),O(0,0),B(8,0),C(7,8),这个四边形的面积.