题目内容
9.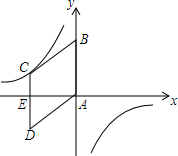 如图,在平面直角坐标系中,菱形ABCD的顶点A与原点O重合,点B在y轴的正半轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,点D的坐标为(-4,-3),CD与x轴交于点E,求k的值.
如图,在平面直角坐标系中,菱形ABCD的顶点A与原点O重合,点B在y轴的正半轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,点D的坐标为(-4,-3),CD与x轴交于点E,求k的值.
分析 直接利用勾股定理进而得出AD的长,再利用菱形的性质得出C点坐标,进而得出k的值.
解答 解:∵点D的坐标为(-4,-3),
∴AE=4,DE=3,
∴AD=5,
∵四边形ABCD为菱形,
∴CD=AD=5,
则EC=2,
∴点C的坐标为(-4,2),
∴k=xy=-8.
点评 此题主要考查了反比例函数综合以及菱形的性质、勾股定理等知识,根据题意得出C点坐标是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列图案中,不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4. 如图,抛物线与x轴的两个交点A(-3,0),B(1,0),则由图象可知y<0时,x的取值范围是( )
如图,抛物线与x轴的两个交点A(-3,0),B(1,0),则由图象可知y<0时,x的取值范围是( )
 如图,抛物线与x轴的两个交点A(-3,0),B(1,0),则由图象可知y<0时,x的取值范围是( )
如图,抛物线与x轴的两个交点A(-3,0),B(1,0),则由图象可知y<0时,x的取值范围是( )| A. | -3<x<1 | B. | x>1 | C. | x<-3 | D. | 0<x<1 |
1.下列大小比较正确的是( )
| A. | -100>0.01 | B. | -6>-5 | C. | -1>-2 | D. | -0.1>0 |
19.把前2015个数1,2,3,…,2015的每一个数的前面任意填上“+”号或“-”号,然后将它们相加,则所得之结果为( )
| A. | 正数 | B. | 奇数 | ||
| C. | 偶数 | D. | 有时为奇数;有时为偶数 |
 如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,点D在BC所在的直线上运动,作∠ADE=45°(A,D,E按逆时针方向).若点D在线段BC上运动,DE交AC于E.
如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,点D在BC所在的直线上运动,作∠ADE=45°(A,D,E按逆时针方向).若点D在线段BC上运动,DE交AC于E.