题目内容
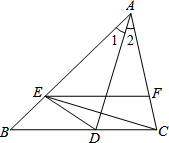 如图,在△ABC中,已知AD平分∠BAC,E是边AB上的一点,AE=AC,F是边AC上的一点,联结DE、CE、FE,当EC平分∠DEF时,猜测EF、BC的位置关系,并说明理由.
如图,在△ABC中,已知AD平分∠BAC,E是边AB上的一点,AE=AC,F是边AC上的一点,联结DE、CE、FE,当EC平分∠DEF时,猜测EF、BC的位置关系,并说明理由.解:EF、BC的位置关系是
说理如下:
因为AD是∠BAC的角平分线(已知)
所以∠1=∠2.
在△AED和△ACD中,
|
所以△AED≌△ACD(S.A.S).
得
(完成以下说理过程)
考点:全等三角形的判定与性质
专题:推理填空题
分析:由AD是∠BAC的角平分线,可得∠1=∠2,利用SAS可证出△AED≌△ACD,从而得出DE=DC,所以∠3=∠4.结合EC平分∠DEF,可得出∠3=∠5.利用等量代换得∠4=∠5,即可得出EF∥BC.
解答:解:EF、BC的位置关系是EF∥BC.
理由如下:
如图,
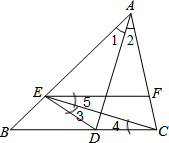
∵AD是∠BAC的角平分线(已知)
∴∠1=∠2.
在△AED和△ACD中,
∴△AED≌△ACD(SAS).
∴DE=DC (全等三角形的对应边相等),
∴∠3=∠4.
∵EC平分∠DEF(已知),
∴∠3=∠5.
∴∠4=∠5.
所以EF∥BC(内错角相等,两直线平行).
故答案为:EF∥BC,DE=DC.
理由如下:
如图,

∵AD是∠BAC的角平分线(已知)
∴∠1=∠2.
在△AED和△ACD中,
|
∴△AED≌△ACD(SAS).
∴DE=DC (全等三角形的对应边相等),
∴∠3=∠4.
∵EC平分∠DEF(已知),
∴∠3=∠5.
∴∠4=∠5.
所以EF∥BC(内错角相等,两直线平行).
故答案为:EF∥BC,DE=DC.
点评:本题主要考查了全等三角形的判定与性质,解题的关键是得出△AED≌△ACD.

练习册系列答案
相关题目
某小组同学聚会,见面时相互间均握了一次手,好事者统计:一共握了36次.你认为这次聚会的同学有( )人.
| A、7 | B、8 | C、9 | D、10 |
若抛物线y=ax2+bx+c的对称轴是x=-2,则
等于( )
| a |
| b |
| A、2 | ||
B、
| ||
| C、4 | ||
D、
|
 如图,将一副直角三角板放在一起,使直角顶点重合于点O.
如图,将一副直角三角板放在一起,使直角顶点重合于点O.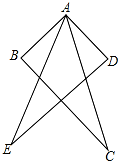 如图,AB=AD,AE=AC,∠BAE=∠DAC,求证:BC=DE.
如图,AB=AD,AE=AC,∠BAE=∠DAC,求证:BC=DE.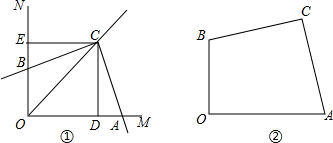
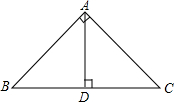 如图所示,∠BAC=90°,AD⊥BC,垂足为D,则给出下列结论:
如图所示,∠BAC=90°,AD⊥BC,垂足为D,则给出下列结论: