题目内容
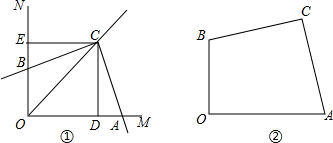
【感知】如图①,∠MON=90°,OC平分∠MON.CD⊥OM于点D,CE⊥ON于点E,可知OD=OE.(不要求证明)
【拓展】在图①中,作∠ACB=90°,CA,CB分别交射线OM,ON于A,B两点,求证:AD=BE.
【应用】如图②,△OAB与△ABC均为直角三角形,OC平分∠AOB,O,C两点在AB的异侧.已知∠AOB=∠ACB=90°,OA=5,OB=3,求线段OC的长.
【拓展】在图①中,作∠ACB=90°,CA,CB分别交射线OM,ON于A,B两点,求证:AD=BE.
【应用】如图②,△OAB与△ABC均为直角三角形,OC平分∠AOB,O,C两点在AB的异侧.已知∠AOB=∠ACB=90°,OA=5,OB=3,求线段OC的长.

考点:全等三角形的判定与性质,勾股定理,矩形的判定与性质
专题:
分析:[拓展]如图①,证明CD=CE;证明∠BCE=∠ACD;证明△ACD≌△BCE,得到AD=BE.
[应用]如图②,作辅助线;类比(1)中的结论得到:OM=ON;结合OA=5,OB=3,得到5-λ=3+λ,λ=1;运用勾股定理即可解决问题.
[应用]如图②,作辅助线;类比(1)中的结论得到:OM=ON;结合OA=5,OB=3,得到5-λ=3+λ,λ=1;运用勾股定理即可解决问题.
解答: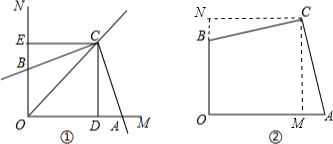 解:【拓展】
解:【拓展】
∵OC平分∠MON,CD⊥OM,CE⊥ON,
∴CD=CE,∠CEB=∠CDA;
∵∠DOE=90°,
∴四边形ODCE为正方形,
∴∠DCE=90°,CD=CE;
∵∠BCA=90°,
∴∠BCE=∠ACD;
在△ACD与△BCE中,
,
∴△ACD≌△BCE(ASA),
∴AD=BE.
【应用】如图②,过点C作CM⊥OA;
CN⊥OB,交OB的延长线于点N;
由(1)知:AM=BN(设为λ),
四边形OMCN为正方形,
∴OM=ON;而OA=5,OB=3,
∴5-λ=3+λ,λ=1,
∴OM=CM=4;
由勾股定理得:OC2=42+42,
∴OC=4
.
 解:【拓展】
解:【拓展】∵OC平分∠MON,CD⊥OM,CE⊥ON,
∴CD=CE,∠CEB=∠CDA;
∵∠DOE=90°,
∴四边形ODCE为正方形,
∴∠DCE=90°,CD=CE;
∵∠BCA=90°,
∴∠BCE=∠ACD;
在△ACD与△BCE中,
|
∴△ACD≌△BCE(ASA),
∴AD=BE.
【应用】如图②,过点C作CM⊥OA;
CN⊥OB,交OB的延长线于点N;
由(1)知:AM=BN(设为λ),
四边形OMCN为正方形,
∴OM=ON;而OA=5,OB=3,
∴5-λ=3+λ,λ=1,
∴OM=CM=4;
由勾股定理得:OC2=42+42,
∴OC=4
| 2 |
点评:该题主要考查了全等三角形的判定及其性质、正方形的判定及其性质、勾股定理等几何知识点及其应用问题;解题的关键是牢固掌握全等三角形的判定等几何知识点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
数轴上的点A表示的数是-1,将点A向左移动5个单位,终点表示的数是( )
| A、4 | B、-4 | C、6 | D、-6 |
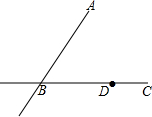 已知:如图,直线AB、BC相交于点B,点D是直线BC上一点.
已知:如图,直线AB、BC相交于点B,点D是直线BC上一点.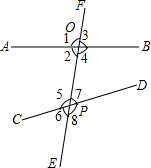 如图,直线AB,CD与直线EF分别交于点O,P.
如图,直线AB,CD与直线EF分别交于点O,P.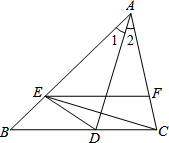 如图,在△ABC中,已知AD平分∠BAC,E是边AB上的一点,AE=AC,F是边AC上的一点,联结DE、CE、FE,当EC平分∠DEF时,猜测EF、BC的位置关系,并说明理由.
如图,在△ABC中,已知AD平分∠BAC,E是边AB上的一点,AE=AC,F是边AC上的一点,联结DE、CE、FE,当EC平分∠DEF时,猜测EF、BC的位置关系,并说明理由. 函数y=ax2与直线y=-2x-4交于点(2,b).
函数y=ax2与直线y=-2x-4交于点(2,b). 某几何体的三视图如图所示,其中主视图中半圆的半径为1.
某几何体的三视图如图所示,其中主视图中半圆的半径为1.