题目内容

若抛物线y=ax2+bx+c的对称轴是x=-2，则
a
b
等于（　　）
A、2
B、
1
2
C、4
D、
1
4
考点：二次函数的性质
专题：
分析：根据二次函数的对称方程可得到-
b
2a
=-2，可求得答案．
解答：解：∵抛物线y=ax2+bx+c的对称轴是x=-2，
∴-
b
2a
=-2，
∴
b
a
=4，
∴
a
b
=
1
4
，
故选D．
点评：本题主要考查二次函数的对称轴方程，掌握二次函数y=ax2+bx+c的对称轴是x=-
b
2a
是解题的关键．
练习册系列答案
相关题目
已知：BE⊥CD，BE=DE，BC=DA，求证：∠B=∠D．
如图所示，在一边靠墙（墙足够长）的空地上，修建一个面积为640m2的矩形临时仓库，仓库一边靠墙，另三边用总长为80m的栅栏围成，若设栅栏AB的长为xm，则下列各方程中，符合题意的是（　　）
A、
1
2
x（80-x）=640
B、
1
2
x（80-2x）=640
C、x（80-2x）=640
D、x（80-x）=640
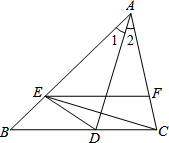如图，在△ABC中，已知AD平分∠BAC，E是边AB上的一点，AE=AC，F是边AC上的一点，联结DE、CE、FE，当EC平分∠DEF时，猜测EF、BC的位置关系，并说明理由．
解：EF、BC的位置关系是
 
．
说理如下：
因为AD是∠BAC的角平分线（已知）
所以∠1=∠2．
在△AED和△ACD中，
AE=AC(已知)
∠()=∠()
()=()(公共边)

所以△AED≌△ACD（S．A．S）．
得
 
（全等三角形的对应边相等）．
（完成以下说理过程）
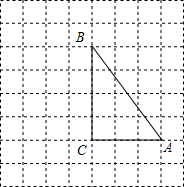如图所示的网格中，每个小网格都是边长为1的正方形，每个小正方形的顶点叫格点，△ABC的顶点都在格点上．在AC的延长线上取一点D，D也在格点上，并连接BD．
（1）如果AC=CD，则△ABD是
 
三角形；
（2）如果△ABD是以BD为底的等腰三角形，求△ABD的周长．
函数y=ax2与直线y=-2x-4交于点（2，b）．
（1）求a和b的值；
（2）写出抛物线的顶点坐标和对称轴；画出此二次函数的图象；
（3）函数y=ax2，当x取何值时，y随x的增大而增大？
……
……
抛物线y=-x2+2x+2绕它与y轴的交点旋转180°后得到的抛物线解析式为（　　）
A、y=x2+2x+2
B、y=-x2-2x+2
C、y=x2+2x+1
D、y=2x2+4x+2
请举一个抽样调查的实例：
 
．
下列说法正确的是（　　）
A、整数和负数统称为有理数
B、0是最小的有理数
C、互为相反数的两数之和为零
D、负数就是有负号的数

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网