题目内容
某小组同学聚会,见面时相互间均握了一次手,好事者统计:一共握了36次.你认为这次聚会的同学有( )人.
| A、7 | B、8 | C、9 | D、10 |
考点:一元二次方程的应用
专题:
分析:可设这次聚会的同学有x人,每个人都与其他(x-1)人握手,共握手次数为
x(x-1),根据一共握了36次手列出方程求解.
| 1 |
| 2 |
解答:解:设这次聚会的同学有x人,依题意得,
x(x-1)=36,
整理,得x2-x-72=0,
解得x1=9,x2=-8(舍去).
则这次聚会的同学有9人.
故选C.
| 1 |
| 2 |
整理,得x2-x-72=0,
解得x1=9,x2=-8(舍去).
则这次聚会的同学有9人.
故选C.
点评:考查了一元二次方程的应用,计算握手次数时,每两个人之间产生一次握手现象,故共握手次数为
x(x-1).
| 1 |
| 2 |

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 小花用围棋子摆正方形,第1,2,3,4个分别如图所示,按这样的规律往下摆,第10个正方形需要的棋子枚数是( )
小花用围棋子摆正方形,第1,2,3,4个分别如图所示,按这样的规律往下摆,第10个正方形需要的棋子枚数是( )| A、44枚 | B、40枚 |
| C、36枚 | D、32枚 |
 如图所示,在一边靠墙(墙足够长)的空地上,修建一个面积为640m2的矩形临时仓库,仓库一边靠墙,另三边用总长为80m的栅栏围成,若设栅栏AB的长为xm,则下列各方程中,符合题意的是( )
如图所示,在一边靠墙(墙足够长)的空地上,修建一个面积为640m2的矩形临时仓库,仓库一边靠墙,另三边用总长为80m的栅栏围成,若设栅栏AB的长为xm,则下列各方程中,符合题意的是( )A、
| ||
B、
| ||
| C、x(80-2x)=640 | ||
| D、x(80-x)=640 |
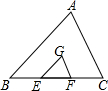 如图,点G是△ABC的重心,过G作CG∥AB,交BC于点E,GF∥AC,交AB于点F,则S△GEF:S△ABC=
如图,点G是△ABC的重心,过G作CG∥AB,交BC于点E,GF∥AC,交AB于点F,则S△GEF:S△ABC= 已知:BE⊥CD,BE=DE,BC=DA,求证:∠B=∠D.
已知:BE⊥CD,BE=DE,BC=DA,求证:∠B=∠D. 如图,直线L⊥n,作一条直线,使它与直线L、n围成的直角三角形的面积是6,且这个直角三角形的一条直角边为3,则这样的直线最多可以作
如图,直线L⊥n,作一条直线,使它与直线L、n围成的直角三角形的面积是6,且这个直角三角形的一条直角边为3,则这样的直线最多可以作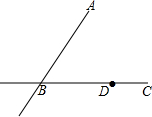 已知:如图,直线AB、BC相交于点B,点D是直线BC上一点.
已知:如图,直线AB、BC相交于点B,点D是直线BC上一点.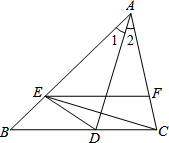 如图,在△ABC中,已知AD平分∠BAC,E是边AB上的一点,AE=AC,F是边AC上的一点,联结DE、CE、FE,当EC平分∠DEF时,猜测EF、BC的位置关系,并说明理由.
如图,在△ABC中,已知AD平分∠BAC,E是边AB上的一点,AE=AC,F是边AC上的一点,联结DE、CE、FE,当EC平分∠DEF时,猜测EF、BC的位置关系,并说明理由.