题目内容
15.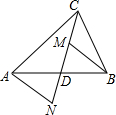 如图,CD为△ABC的中线,M、N分别为直线CD上的点,且BM∥AN.
如图,CD为△ABC的中线,M、N分别为直线CD上的点,且BM∥AN.(1)求证:AN=BM;
(2)求证:CM+CN=2CD.
分析 (1)证明△AND≌△BMD即可;
(2)由△AND≌△BMD可知DM=DN,则CM+CN=2CD.
解答 证明:(1)∵CD为△ABC的中线,
∴AD=BD,
∵BM∥AN,
∴∠AND=∠BMD,
在△AND和△BMD中,
$\left\{\begin{array}{l}{∠AND=∠BMD}\\{∠ADN=∠BDM}\\{AD=BD}\end{array}\right.$,
∴△AND≌△BMD(AAS),
∴AN=BM;
(2)∵△AND≌△BMD,
∴DM=DN,
∵CM+CN=CM+CM+DM+DN,
∴CM+CN=CM+CM+DM+DM=2(CM+DM)=2CD.
点评 本题主要考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解决问题的关键.

练习册系列答案
相关题目
7.Rt△ABC中,∠C=90°,如果各边的长度都扩大到原来的2倍,那么sinA的值( )
| A. | 都扩大到原来的2倍 | B. | 都缩小到原来的一半 | ||
| C. | 没有变化 | D. | 不能确定 |
 如图,△ABC为等边三角形,点P(x,y)在△ABC内随机移动,求x>y的概率.
如图,△ABC为等边三角形,点P(x,y)在△ABC内随机移动,求x>y的概率.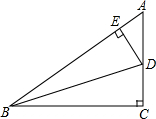 在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,若AB=10,BC=8,AC=6,求△AED的周长.
在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,若AB=10,BC=8,AC=6,求△AED的周长.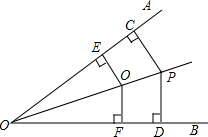 如图,PC⊥OA于点C,PD⊥OB于点D,PC=PD,Q是OP上一点,QE⊥OA于点E,QF⊥OB于点F,求证:QE=QF.
如图,PC⊥OA于点C,PD⊥OB于点D,PC=PD,Q是OP上一点,QE⊥OA于点E,QF⊥OB于点F,求证:QE=QF.