题目内容
3.已知α,β都是锐角,且α+β=90°,sinα+cosβ=$\sqrt{3}$,则α=60°.分析 根据互余两角的三角函数的关系得出cosβ=sinα,求出sinα=$\frac{\sqrt{3}}{2}$,即可得出答案.
解答 解:∵α+β=90°,
∴cosβ=sinα,
∵sinα+cosβ=$\sqrt{3}$,
2sinα=$\sqrt{3}$,
sinα=$\frac{\sqrt{3}}{2}$,
∴锐角α=60°.
故答案为60°.
点评 本题考查了互余两角的三角函数的关系,特殊角的三角函数值的应用,解此题的关键是求出sinα的值.

练习册系列答案
相关题目
13.下列各式中正确的是( )
| A. | $\sqrt{4}$=±2 | B. | $\sqrt{{3^2}+{4^2}}$=7 | C. | $\sqrt{(-\frac{1}{2}}{)^2}=-\frac{1}{2}$ | D. | $\sqrt{2\frac{1}{4}}=1\frac{1}{2}$ |




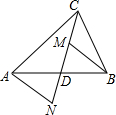 如图,CD为△ABC的中线,M、N分别为直线CD上的点,且BM∥AN.
如图,CD为△ABC的中线,M、N分别为直线CD上的点,且BM∥AN.
 如图,四边形OABC与四边形OA′B′C′是位似图形,AB与A′B′一定平行吗?为什么?
如图,四边形OABC与四边形OA′B′C′是位似图形,AB与A′B′一定平行吗?为什么?