题目内容
4. 如图,△ABC内接于圆O,半径R=$\sqrt{2}$+1,圆I过O,且与AB、AC相切,圆I的半径r=1,求证:圆I是△ABC的内切圆.
如图,△ABC内接于圆O,半径R=$\sqrt{2}$+1,圆I过O,且与AB、AC相切,圆I的半径r=1,求证:圆I是△ABC的内切圆.
分析 作直线OI交⊙O于EF,延长AI交⊙O于M,连接MC,BC,连接OM交BC于K,连接OC,根据切线性质得到AM平分∠BAC,设∠BAM=∠BCM=α,由三角函数的定义得到AI=$\frac{DI}{sinα}$,根据勾股定理得到CM=2($\sqrt{2}$+1)sinα,求得IM=CM,根据等腰三角形的性质得到∠MIC=∠MCI,推出∠ACI=∠BCI,于是得到结论.
解答  解:作直线OI交⊙O于EF,延长AI交⊙O于M,连接MC,BC,连接OM交BC于K,连接OC,
解:作直线OI交⊙O于EF,延长AI交⊙O于M,连接MC,BC,连接OM交BC于K,连接OC,
∵⊙O与AB、AC相切,
∴AM平分∠BAC,
设∠BAM=∠BCM=α,
∴AI=$\frac{DI}{sinα}$,
∵AI•IM=EI•IF=($\sqrt{2}$+1+1)$•\sqrt{2}$=2($\sqrt{2}$+1),IM=2($\sqrt{2}$+1)•sinα,
∵OM=OC=$\sqrt{2}$+1,KM=CM•sinα,KC=CM•cosα,
∵OK2+CK2=OC2,[($\sqrt{2}$+1)-cm•sinα]2+CM2cos2α=($\sqrt{2}$+1)2,($\sqrt{2}$+1)2-2($\sqrt{2}+$10•CM•sinα+CM2sin2α+CM2cos2α=($\sqrt{2}$+1)2,
∵CM2sin2α+CM2cos2α=CM2,
∴CM=2($\sqrt{2}$+1)sinα,
∴IM=CM,
∴∠MIC=∠MCI,
∴∠MAC+∠ACI=∠MCB+∠BCI,
∴∠ACI=∠BCI,
∴I是⊙I的内心,⊙I是△ABC的内切圆.
点评 本题考查了三角形的内切圆与内心,三角形的外切圆与外心,等腰三角形的判定与性质,切线的性质,三角函数的定义,勾股定理,正确的作出辅助线是解题的关键.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案 如图,已知∠1=25°,∠AOC=90°,点B、O、D在同一直线上,则∠2的度数为( )
如图,已知∠1=25°,∠AOC=90°,点B、O、D在同一直线上,则∠2的度数为( )| A. | 155° | B. | 125° | C. | 115° | D. | 65° |
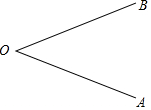 如图,∠AOB
如图,∠AOB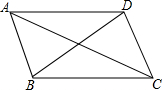 如图,给出下列四个条件:①AC=BD;②∠DAC=∠BCA;③∠ABD=∠CDB;④∠ADB=∠CBD,其中能使AD∥BC的条件为( )
如图,给出下列四个条件:①AC=BD;②∠DAC=∠BCA;③∠ABD=∠CDB;④∠ADB=∠CBD,其中能使AD∥BC的条件为( )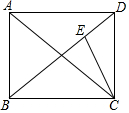 如图,在矩形ABCD中,已知AB=6,BC=8.连接AC,BD,CE平分∠ACD交BD于点E,则DE=$\frac{30}{11}$.
如图,在矩形ABCD中,已知AB=6,BC=8.连接AC,BD,CE平分∠ACD交BD于点E,则DE=$\frac{30}{11}$.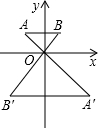 如图,已知△OAB与△OA′B′是相似比为1:2的位似图形,点O是位似中心,若OA=2,则AA′的长是( )
如图,已知△OAB与△OA′B′是相似比为1:2的位似图形,点O是位似中心,若OA=2,则AA′的长是( )