题目内容
19.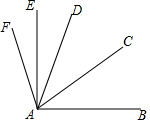 如图,∠FAB=106°,AE是∠FAD的平分线,AC是∠DAB的平分线,∠EAD=20°.下列关系错误的是( )
如图,∠FAB=106°,AE是∠FAD的平分线,AC是∠DAB的平分线,∠EAD=20°.下列关系错误的是( )| A. | ∠FAD=40° | B. | ∠CAB=33° | C. | ∠FAB=2∠EDC | D. | ∠EAD与∠DAB互余 |
分析 由AE是∠FAD的平分线,得到∠EAF=∠DAE=20°,∠DAF=2∠DAE=40°,故A正确;于是得到∠EAD+∠DAB=86°,故D错误;由AC是∠DAB的平分线,得到∠CAB=∠CAD=$\frac{1}{2}∠$BAD=33°,故B正确;求得∠CAE=∠DAE+∠CAD=53°,于是得到∠FAB=2∠EDC,故③正确.
解答 解:∵AE是∠FAD的平分线,
∴∠EAF=∠DAE=20°,∠DAF=2∠DAE=40°,故A正确;
∴∠BAE=∠FAB-∠EAF=86°,∠BAD=66°,
∴∠EAD+∠DAB=86°,故D错误;
∵AC是∠DAB的平分线,
∴∠CAB=∠CAD=$\frac{1}{2}∠$BAD=33°,故B正确;
∴∠CAE=∠DAE+∠CAD=53°,
∴∠FAB=2∠EDC,故③正确;
故选D.
点评 本题考查了余角和补角,角平分线的定义,熟练掌握角平分线的定义是解题的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
10. 如图,已知△ABC≌△BAD,F是AB的中点,则图中全等三角形共有( )
如图,已知△ABC≌△BAD,F是AB的中点,则图中全等三角形共有( )
 如图,已知△ABC≌△BAD,F是AB的中点,则图中全等三角形共有( )
如图,已知△ABC≌△BAD,F是AB的中点,则图中全等三角形共有( )| A. | 一组 | B. | 二组 | C. | 三组 | D. | 四组 |
14. 如图,已知∠1=25°,∠AOC=90°,点B、O、D在同一直线上,则∠2的度数为( )
如图,已知∠1=25°,∠AOC=90°,点B、O、D在同一直线上,则∠2的度数为( )
 如图,已知∠1=25°,∠AOC=90°,点B、O、D在同一直线上,则∠2的度数为( )
如图,已知∠1=25°,∠AOC=90°,点B、O、D在同一直线上,则∠2的度数为( )| A. | 155° | B. | 125° | C. | 115° | D. | 65° |
 如图是一个正方体展开图,如果把这个展开图折叠成正方体,那么所得正方体中,“国”字一面相对面上的字是“的”
如图是一个正方体展开图,如果把这个展开图折叠成正方体,那么所得正方体中,“国”字一面相对面上的字是“的”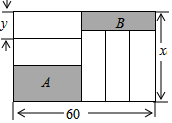 如图,长为60cm,宽为x(cm)的大长方形被分割为7小块,除阴影 A,B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为 y(cm).
如图,长为60cm,宽为x(cm)的大长方形被分割为7小块,除阴影 A,B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为 y(cm).