题目内容
13.如图在矩形ABCD中,AB=nAD,点E、F分别在AB、AD上且不与顶点A、B、D重合,∠AEF=∠BCE,圆O过A、E、F三点.(1)求证:圆O与CE相切于点E.
(2)如图1,若AF=2FD,且∠AEF=30°,求n的值.
(3)如图2,若EF=EC,且圆O与边CD相切,求n的值.
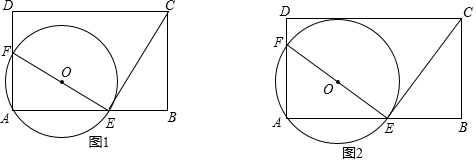
分析 (1)根据已知条件得到∠BEC+∠BCE=90°,等量代换得到∠AEF+∠BEC=90°,求得∠FEC=90°,于是得到结论;
(2)设DF=x,则AF=2x,得到BC=AD=3x,解直角三角形得到AE=$\sqrt{3}$AF=2$\sqrt{3}$x,根据相似三角形的性质得到BE=$\sqrt{3}$x,求得AB=AE+BE=3$\sqrt{3}$x,根据已知条件列方程即可得到结论;
(3)如图2,设CD与⊙O相切于G,连接GO并延长交AE于H,连接OC.根据切线的性质得到HG⊥CD,推出四边形AHGD是矩形,根据矩形的性质得到GH=AD=BC,AH=HE=DG,设OG=OF=OE=R,OH=x,求得AD=GH=BC=R+x,AF=2x,根据全等三角形的性质得到BE=AF=2x,CE=EF=2R,AE=BC=R+x,求得AB=R+3x,根据切线的性质得到CG=CE=BH=2R,得到AB=AH+BH=$\frac{5R+x}{2}$,然后列方程即可得到结论.
解答 解:(1)∵在矩形ABCD中,∠B=90°,
∴∠BEC+∠BCE=90°,
∵∠AEF=∠BCE,
∴∠AEF+∠BEC=90°,
∴∠FEC=90°,
∴FE⊥CE,
∴圆O与CE相切于点E;
(2)∵AF=2FD,
∴设DF=x,则AF=2x,
∴BC=AD=3x,
∵∠AEF=30°,∠A=90°,
∴AE=$\sqrt{3}$AF=2$\sqrt{3}$x,
∵∠A=∠B=90°,∠AEF=∠BCE,
∴△AEF∽△BCE,
∴$\frac{AF}{BE}=\frac{AE}{BC}$,即$\frac{2x}{BE}=\frac{2\sqrt{3}x}{3x}$,
∴BE=$\sqrt{3}$x,
∴AB=AE+BE=3$\sqrt{3}$x,
∵AB=nAD,
∴3$\sqrt{3}$x=n•3x,
∴n=$\sqrt{3}$;
(3)如图2,设CD与⊙O相切于G,连接GO并延长交AE于H,
连接OC.
∵CD与⊙O相切于G,
∴HG⊥CD,
∵CD∥AB,
∴GH⊥AB,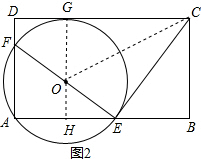
∴四边形AHGD是矩形,
∴GH=AD=BC,AH=HE=DG,
设OG=OF=OE=R,OH=x,
∴AD=GH=BC=R+x,AF=2x,
在△AEF与△BCE中,$\left\{\begin{array}{l}{∠A=∠B=90°}\\{∠AEF=∠BCE}\\{EF=EC}\end{array}\right.$,
∴△AEF≌△BCE,
∴BE=AF=2x,CE=EF=2R,AE=BC=R+x,
∴AB=R+3x,
∵CG和CE是⊙O的切线,
∴CG=CE=BH=2R,
∵AH=$\frac{1}{2}$AE=$\frac{R+x}{2}$,
∴AB=AH+BH=$\frac{5R+x}{2}$,
∴R+3x=$\frac{5R+x}{2}$,
∴R=$\frac{5}{3}$x,
∴AD=$\frac{8}{3}$x,AB=$\frac{14x}{3}$,
∵AB=nAD,
∴$\frac{14}{3}$x=n•$\frac{8}{3}$x,
∴n=$\frac{7}{4}$.
点评 本题考查了切线的性质,矩形的性质,全等三角形的判定和性质,相似三角形的判定和性质,正确的作出辅助线是解题的关键.

| 课题:测量古塔的高度 | ||
| 小明的研究报告 | 小红的研究报告 | |
| 图示 | 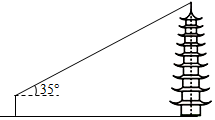 | 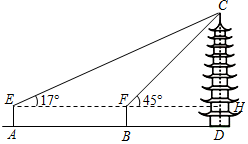 |
| 测量方案与测量数据 | 用距离地面高度为1.6m的测角器测出古塔顶端的仰角为35°,再用皮尺测得测角器所在位置与古塔底部边缘的最短距离为30m. | 在点A用距离地面高度为1.6m的测角器测出古塔顶端的仰角为17°,然后沿AD方向走58.8m到达点B,测出古塔顶端的仰角为45°. |
| 参考数据 | sin35°≈0.57,cos35°≈0.82,tan35°≈0.70 | sin17°≈0.29,cos17°≈0.96,tan17°≈0.30,$\sqrt{2}$≈1.41 |
| 计算古塔高度 (结果精确到0.1m) | 30×tan35°+1.6≈22.6(m) | |
(2)数学老师说小红的结果较准确,而小明的结果与古塔的实际高度偏差较大.针对小明的测量方案分析测量发生偏差的原因;
(3)利用小明与小红的测量数据,估算该古塔底面圆直径的长度为8.4m.
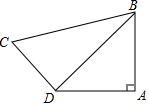 如图:四边形ABCD中,AB=4,BC=2$\sqrt{10}$,CD=2$\sqrt{2}$,AD=4,∠A=90°,求∠ADC的度数.
如图:四边形ABCD中,AB=4,BC=2$\sqrt{10}$,CD=2$\sqrt{2}$,AD=4,∠A=90°,求∠ADC的度数.
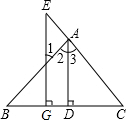 如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,试说明AD平分∠BAC.完成下面推理过程:
如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,试说明AD平分∠BAC.完成下面推理过程: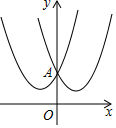 如果两个二次函数的图象关于y轴对称,我们就称这两个二次函数互为“关于y轴对称二次函数”,如图所示二次函数y1=x2+2x+2与y2=x2-2x+2是“关于y轴对称二次函数”.
如果两个二次函数的图象关于y轴对称,我们就称这两个二次函数互为“关于y轴对称二次函数”,如图所示二次函数y1=x2+2x+2与y2=x2-2x+2是“关于y轴对称二次函数”.