题目内容
1.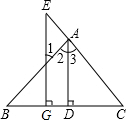 如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,试说明AD平分∠BAC.完成下面推理过程:
如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,试说明AD平分∠BAC.完成下面推理过程:证明:∵AD⊥BC于D,EG⊥BC于G(已知)
∴∠ADC=∠EGC=90° (垂直的定义)
∴AD∥EG (同位角相等,两直线平行)
∴∠1=∠2 (两直线平行,内错角相等)
∠E=∠3 (两直线平行,同位角相等)
又∵∠E=∠1(已知)
∴∠2=∠3 (等量代换)
∴AD平分∠BAC (角平分线的定义).
分析 先根据垂直的定义得出∠ADC=∠EGC=90°,故可得出AD∥EG,再由平行线的性质可知∠1=∠2,∠E=∠3,故可得出∠2=∠3,据此可得出结论.
解答 证明:∵AD⊥BC于D,EG⊥BC于G(已知),
∴∠ADC=∠EGC=90° (垂直的定义).
∴AD∥EG (同位角相等,两直线平行),
∴∠1=∠2 (两直线平行,内错角相等),
∠E=∠3 (两直线平行,同位角相等).
又∵∠E=∠1(已知),
∴∠2=∠3 (等量代换),
∴AD平分∠BAC (角平分线的定义).
故答案为:垂直的定义;同位角相等,两直线平行;两直线平行,内错角相等;两直线平行,同位角相等;等量代换; 角平分线的定义.
点评 本题考查的是平行线的判定与性质,熟知平行线的判定定理是解答此题的关键.

练习册系列答案
相关题目
11. 张老师在黑板上画出了如图所示的图形,已知∠BAC=90°,AD⊥BC,垂足为D,则下列说法错误的是( )
张老师在黑板上画出了如图所示的图形,已知∠BAC=90°,AD⊥BC,垂足为D,则下列说法错误的是( )
 张老师在黑板上画出了如图所示的图形,已知∠BAC=90°,AD⊥BC,垂足为D,则下列说法错误的是( )
张老师在黑板上画出了如图所示的图形,已知∠BAC=90°,AD⊥BC,垂足为D,则下列说法错误的是( )| A. | ∠BAC与∠B是同旁内角 | B. | AB与AC互相垂直 | ||
| C. | 点A与直线BC的垂线段为线段AD | D. | 点A到BC的距离是线段AD |
12.下列说法中,正确的是( )
| A. | 两点之间的连线中,直线最短 | |
| B. | 若AP=BP,则P是线段AB的中点 | |
| C. | 若P是线段AB的中点,则AP=BP | |
| D. | 两点之间的线段叫做这两点之间的距离 |
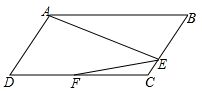 如图,已知?ABCD中,AB=2BC,AE⊥BC于E,F是CD的中点,∠FEC=54°,求∠B的度数.
如图,已知?ABCD中,AB=2BC,AE⊥BC于E,F是CD的中点,∠FEC=54°,求∠B的度数. 在平面直角坐标系中,A、B、C三点的坐标分别为:A(-5,5)、B(-3,0)、C(0,3).
在平面直角坐标系中,A、B、C三点的坐标分别为:A(-5,5)、B(-3,0)、C(0,3).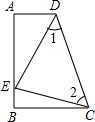 如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
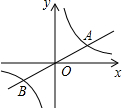 已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A、B两点,且点A的横坐标为4.
已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A、B两点,且点A的横坐标为4.