题目内容
3.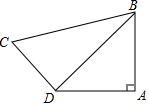 如图:四边形ABCD中,AB=4,BC=2$\sqrt{10}$,CD=2$\sqrt{2}$,AD=4,∠A=90°,求∠ADC的度数.
如图:四边形ABCD中,AB=4,BC=2$\sqrt{10}$,CD=2$\sqrt{2}$,AD=4,∠A=90°,求∠ADC的度数.
分析 根据等腰直角三角形的性质得到∠ADB=45°,根据勾股定理得BD2=AB2+AD2=32,根据勾股定理逆定理得△BDC是直角三角形.于是得到结论.
解答 解:在△ABD中,∠A=90°,AB=4,AD=4
∴∠ADB=45°,
根据勾股定理得BD2=AB2+AD2=32,
∵BC=2$\sqrt{10}$,CD=2$\sqrt{2}$,
∴BC2=40,CD2=8,
∴BC2=CD2+BD2,
根据勾股定理逆定理得△BDC是直角三角形,∠BDC=90°,
∴∠ADC=∠ADB+∠BDC=135°.
点评 本题考查了勾股定理的逆定理,勾股定理,熟练掌握勾股定理的逆定理是解题的关键.

练习册系列答案
相关题目
14.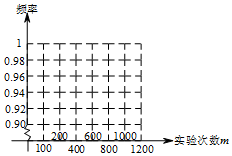 某批足球的质量检测结果如下:
某批足球的质量检测结果如下:
(1)填写表中的空格.(结果保留0.01)
(2)画出合格的频率的折线统计图.
(3)从这批足球任意抽取的一只足球是合格品的概率估计值是多少?并说明理由.
 某批足球的质量检测结果如下:
某批足球的质量检测结果如下:| 抽取足球数n | 100 | 200 | 400 | 600 | 800 | 1000 |
| 合格的频数m | 93 | 192 | 384 | 564 | 759 | 950 |
| 合格的频率$\frac{m}{n}$ | 0.93 | 0.96 | 0.96 | 0.94 | 0.95 | 0.95 |
(2)画出合格的频率的折线统计图.
(3)从这批足球任意抽取的一只足球是合格品的概率估计值是多少?并说明理由.
11. 张老师在黑板上画出了如图所示的图形,已知∠BAC=90°,AD⊥BC,垂足为D,则下列说法错误的是( )
张老师在黑板上画出了如图所示的图形,已知∠BAC=90°,AD⊥BC,垂足为D,则下列说法错误的是( )
 张老师在黑板上画出了如图所示的图形,已知∠BAC=90°,AD⊥BC,垂足为D,则下列说法错误的是( )
张老师在黑板上画出了如图所示的图形,已知∠BAC=90°,AD⊥BC,垂足为D,则下列说法错误的是( )| A. | ∠BAC与∠B是同旁内角 | B. | AB与AC互相垂直 | ||
| C. | 点A与直线BC的垂线段为线段AD | D. | 点A到BC的距离是线段AD |
8.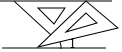 如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
 如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )| A. | 30° | B. | 20° | C. | 15° | D. | 14° |
12.下列说法中,正确的是( )
| A. | 两点之间的连线中,直线最短 | |
| B. | 若AP=BP,则P是线段AB的中点 | |
| C. | 若P是线段AB的中点,则AP=BP | |
| D. | 两点之间的线段叫做这两点之间的距离 |
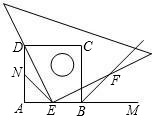 如图所示,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F.
如图所示,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F. 如图,在正方形ABCD中,点E是AD边上的一点,AF⊥BE于F,CG⊥BE于G.
如图,在正方形ABCD中,点E是AD边上的一点,AF⊥BE于F,CG⊥BE于G.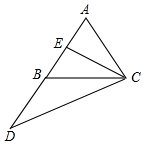 如图,在△ABC中,AB=AC,D是AB延长线上一点,BD=AB,E是AB的中点,求证:CE=$\frac{1}{2}$CD.
如图,在△ABC中,AB=AC,D是AB延长线上一点,BD=AB,E是AB的中点,求证:CE=$\frac{1}{2}$CD.