题目内容
3.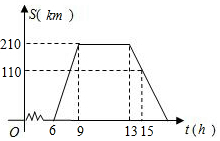 某旅游团上午6时从旅馆出发,乘汽车到距离210km的某著名旅游景点游玩,该汽车离旅馆的距离S(km)与时间t(h)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:
某旅游团上午6时从旅馆出发,乘汽车到距离210km的某著名旅游景点游玩,该汽车离旅馆的距离S(km)与时间t(h)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:(1)求该团去景点时的平均速度是多少?
(2)该团在旅游景点游玩了多少小时?
(3)求返回到宾馆的时刻是几时几分?
分析 (1)根据路程除以时间等于速度,可得答案;
(2)根据路程不变,可得相应的自变量的范围;
(3)根据待定系数法,可得函数关系式,根据自变量与函数值得对应关系,可得答案.
解答 解:(1)210÷(9-6)=70(千米/时)
答:该团去景点时的平均速度是70千米/时;
(2)由横坐标得出9时到达景点,13是离开景点,13-9=4小时,
答:该团在旅游景点游玩了4小时;
(3)设返回途中函数关系式是S=kt+b,由题意,得
$\left\{\begin{array}{l}{13t+b=210}\\{15t+b=110}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-50}\\{t=860}\end{array}\right.$,
返回途中函数关系式是S=-50t+860,
当s=0时,t=17.2,
返回到宾馆的时刻是17点12分.
点评 本题考查了函数图象,观察函数图象得出路程与时间的关系是解题关键.

练习册系列答案
相关题目
14.下列计算正确的是( )
| A. | (x-2)2=x2-4 | B. | (m+n)2=m2+n2 | C. | (x+2)(x-2)=x2-4 | D. | (m-n)2=m2-2mn-n2 |
8.甲,乙,丙,丁四名跳高运动员赛前几次选拔赛成绩如表所示,根据表中的信息,如果要从中,选择一名成绩好又发挥稳定的运动员参加比赛,那么应选甲.
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(cm) | 185 | 180 | 185 | 180 |
| 方差 | 3.6 | 3.6 | 7.9 | 8.2 |
15.如果代数式x2+kx+49能分解成(x-7)2形式,那么k的值为( )
| A. | 7 | B. | -14 | C. | ±7 | D. | ±14 |
12. 如图,AB∥CD,CD⊥EF,若∠1=125°,则∠2=( )
如图,AB∥CD,CD⊥EF,若∠1=125°,则∠2=( )
 如图,AB∥CD,CD⊥EF,若∠1=125°,则∠2=( )
如图,AB∥CD,CD⊥EF,若∠1=125°,则∠2=( )| A. | 25° | B. | 35° | C. | 55° | D. | 65° |
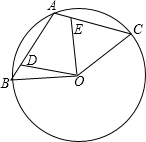 已知A、B、C是圆O上的三个点,其中点A是弧BC的中点,连接AB、AC,点D、E分别在弦AB、AC上,且满足AD=CE.
已知A、B、C是圆O上的三个点,其中点A是弧BC的中点,连接AB、AC,点D、E分别在弦AB、AC上,且满足AD=CE. 如图,在正方形ABCD内有一折线段,其中AE丄EF,EF丄FC,并且AE=3,EF=4,FC=5,则正方形ABCD的外接圆的半径是4$\sqrt{5}$.
如图,在正方形ABCD内有一折线段,其中AE丄EF,EF丄FC,并且AE=3,EF=4,FC=5,则正方形ABCD的外接圆的半径是4$\sqrt{5}$.