题目内容
19. 如图,在△ABC中,已知∠ADE=∠B,则下列等式成立的是( )
如图,在△ABC中,已知∠ADE=∠B,则下列等式成立的是( )| A. | $\frac{AE}{AB}$=$\frac{AD}{AC}$ | B. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | C. | $\frac{DE}{BC}$=$\frac{AE}{AB}$ | D. | $\frac{DE}{BC}$=$\frac{AD}{AC}$ |
分析 首先证明△AED∽△ACB,再根据相似三角形的性质:对应边成比例可得答案.
解答 解:∵∠A=∠A,∠ADE=∠B,
∴△AED∽△ACB,
∴$\frac{AD}{AB}=\frac{AE}{AC}$.
故选:B.
点评 此题主要考查了相似三角形的性质与判定,关键是掌握判断三角形相似的方法和相似三角形的性质.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
9.若(9+x2)(x+3)( )=81-x4,则括号内应填入的代数式为( )
| A. | x-3 | B. | 3-x | C. | 3+x | D. | x-9 |
8. 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,下列结论中$\underset{不}{•}$$\underset{一}{•}$$\underset{定}{•}$正确的是( )
如图,在平行四边形ABCD中,对角线AC,BD相交于点O,下列结论中$\underset{不}{•}$$\underset{一}{•}$$\underset{定}{•}$正确的是( )
 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,下列结论中$\underset{不}{•}$$\underset{一}{•}$$\underset{定}{•}$正确的是( )
如图,在平行四边形ABCD中,对角线AC,BD相交于点O,下列结论中$\underset{不}{•}$$\underset{一}{•}$$\underset{定}{•}$正确的是( )| A. | AB=CD | B. | BO=OD | C. | ∠BAD=∠BCD | D. | AB⊥AC |




 阅读下面材料:
阅读下面材料: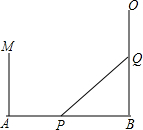 如图,已知AB=20米,MA⊥AB于A,MA=10米,射线BD⊥AB于B,P点从B点向A运动,每秒走2米,Q点从B点向D运动,每秒走3米,P、Q同时从B出发,则出发4秒后,在线段MA上有一点C,使△CAP与△PBQ全等.
如图,已知AB=20米,MA⊥AB于A,MA=10米,射线BD⊥AB于B,P点从B点向A运动,每秒走2米,Q点从B点向D运动,每秒走3米,P、Q同时从B出发,则出发4秒后,在线段MA上有一点C,使△CAP与△PBQ全等.