题目内容
8．
如图，在平行四边形ABCD中，对角线AC，BD相交于点O，下列结论中$\underset{不}{•}$$\underset{一}{•}$$\underset{定}{•}$正确的是（ ）| A． | AB=CD | B． | BO=OD | C． | ∠BAD=∠BCD | D． | AB⊥AC |
分析 由平行四边形的性质容易得出结论．
解答 解：∵四边形ABCD是平行四边形，
∴AB=CD，BO=OD，∠BAD=∠BCD，
∴选项A、B、C、正确，D不一定正确；
故选：D．
点评 本题考查了平行四边形的性质；熟记平行四边形的对边相等、对角相等、对角线互相平分是解决问题的关键．
练习册系列答案
相关题目
18．下列各式中正确的是（ ）
| A． | $\sqrt{9}$=±3 | B． | $\sqrt{-16}$=-4 | C． | （-$\sqrt{3}$）2=9 | D． | $\sqrt{（-5）^{2}}$=5 |
19．
如图，在△ABC中，已知∠ADE=∠B，则下列等式成立的是（ ）
如图，在△ABC中，已知∠ADE=∠B，则下列等式成立的是（ ）| A． | $\frac{AE}{AB}$=$\frac{AD}{AC}$ | B． | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | C． | $\frac{DE}{BC}$=$\frac{AE}{AB}$ | D． | $\frac{DE}{BC}$=$\frac{AD}{AC}$ |
16．已知△ABC的三边长分别为a，b，c，且满足（a-5）2+|b-12|+$\sqrt{c-13}$=0，则△ABC（ ）
| A． | 不是直角三角形 | B． | 是以a为斜边的直角三角形 | ||
| C． | 是以b为斜边的直角三角形 | D． | 是以c为斜边的直角三角形 |
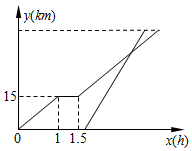周末，小华骑自行车从家出发到植物园玩，从家出发1小时后，因自行车损坏修理了一段时间后，按原速前往植物园，小华从家出发1小时50分后，爸爸从家出发骑摩托车沿相同路线前往植物园，如图是他们家的路程y（km）与小华离家的时间x（h）的函数图象，已知爸爸骑摩托车的速度是小华骑车速度的2倍，若爸爸比小华早10分达到植物园，则小华家到植物园的路程是45km．
17．
尺规作图作∠AOB的平分线方法如下：以O为圆心，任意长为半径画弧交OA、OB于C、D，再分别以点C、D为圆心，以大于$\frac{1}{2}$CD长为半径画弧，两弧交于点P，作射线OP，由作法可得△OCP≌△ODP，判定这两个三角形全等的根据是（ ）
尺规作图作∠AOB的平分线方法如下：以O为圆心，任意长为半径画弧交OA、OB于C、D，再分别以点C、D为圆心，以大于$\frac{1}{2}$CD长为半径画弧，两弧交于点P，作射线OP，由作法可得△OCP≌△ODP，判定这两个三角形全等的根据是（ ）| A． | SAS | B． | ASA | C． | AAS | D． | SSS |
18．下列事件是不可能事件的是（ ）
| A． | 买一张电影票，座位号是奇数 | |
| B． | 从一个只装有红球的袋子里摸出白球 | |
| C． | 三角形两边之和大于第三边 | |
| D． | 明天会下雨 |