题目内容
14．请你用作图工具在下面的数轴上作出表示$\sqrt{10}$的点A和表示1+$\sqrt{2}$的点B，保留作图痕迹，不写作法．
分析 根据勾股定理，作出以3和1为直角边的直角三角形，则其斜边的长即是$\sqrt{10}$；再以原点为圆心，以$\sqrt{10}$为半径画弧与数轴的正半轴的交点即为所求；根据勾股定理，作出以1和1为直角边的直角三角形，则其斜边的长即是$\sqrt{2}$；再以点1为圆心，以$\sqrt{10}$为半径画弧与数轴的正半轴的交点即为所求．
解答 解：如图所示：
点评 本题考查勾股定理及实数与数轴的知识，要求能够正确运用数轴上的点来表示一个无理数，解题关键是构造直角三角形，并灵活运用勾股定理．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
如图，在直角坐标系中，已知△ABC的边BC∥y轴．
5．下面说法正确的是（ ）
| A． | $\frac{1}{4}$和-4互为相反数 | B． | $\frac{1}{4}$和-4互为倒数 | ||
| C． | 0.1和10互为倒数 | D． | 0的倒数是0 |
（1）下列仅用无刻度的直尺就能完成作图的是②（填写序号即可）
19．
如图，在△ABC中，已知∠ADE=∠B，则下列等式成立的是（ ）
如图，在△ABC中，已知∠ADE=∠B，则下列等式成立的是（ ）| A． | $\frac{AE}{AB}$=$\frac{AD}{AC}$ | B． | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | C． | $\frac{DE}{BC}$=$\frac{AE}{AB}$ | D． | $\frac{DE}{BC}$=$\frac{AD}{AC}$ |
6．已知一元二次方程x2+3x+2=0，下列判断正确的是（ ）
| A． | 该方程无实数解 | B． | 该方程有两个相等的实数解 | ||
| C． | 该方程有两个不相等的实数解 | D． | 该方程解的情况不确定 |
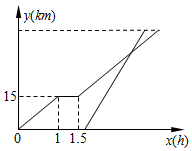周末，小华骑自行车从家出发到植物园玩，从家出发1小时后，因自行车损坏修理了一段时间后，按原速前往植物园，小华从家出发1小时50分后，爸爸从家出发骑摩托车沿相同路线前往植物园，如图是他们家的路程y（km）与小华离家的时间x（h）的函数图象，已知爸爸骑摩托车的速度是小华骑车速度的2倍，若爸爸比小华早10分达到植物园，则小华家到植物园的路程是45km．
4．
如图，直线l1∥l2，∠A=124°，∠B=86°，则∠1+∠2=（ ）
如图，直线l1∥l2，∠A=124°，∠B=86°，则∠1+∠2=（ ）| A． | 30° | B． | 35° | C． | 36° | D． | 40° |