题目内容
 如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO=
如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO=考点:切线的性质
专题:计算题
分析:先根据切线长定理,由AB、AC为⊙O的切线得到∠BAO=∠CAO,根据切线的性质得OB⊥AB,加上BD=OB,则可判断△AOD为等腰三角形,于是根据等腰三角形的性质得∠BAO=∠BAD,即∠CAO=∠BAO=∠BAD,
然后利用∠DAC=∠BAD+∠BAO+∠CAO=78°可计算出∠BAD=26°,再利用∠ADO=90°-∠BAD求解.
然后利用∠DAC=∠BAD+∠BAO+∠CAO=78°可计算出∠BAD=26°,再利用∠ADO=90°-∠BAD求解.
解答:解:∵AB、AC为⊙O的切线,
∴∠BAO=∠CAO,OB⊥AB,
∵BD=OB,
∴△AOD为等腰三角形,
∴∠BAO=∠BAD,
∴∠CAO=∠BAO=∠BAD,
∵∠DAC=∠BAD+∠BAO+∠CAO=78°,
∴3∠BAD=78°,解得∠BAD=26°,
∴∠ADO=90°-∠BAD=90°-26°=64°.
故答案为64°.
∴∠BAO=∠CAO,OB⊥AB,
∵BD=OB,
∴△AOD为等腰三角形,
∴∠BAO=∠BAD,
∴∠CAO=∠BAO=∠BAD,
∵∠DAC=∠BAD+∠BAO+∠CAO=78°,
∴3∠BAD=78°,解得∠BAD=26°,
∴∠ADO=90°-∠BAD=90°-26°=64°.
故答案为64°.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了切线长定理.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
三门峡市大约有二百二十万人,将二百二十万用科学记数法表示为( )
| A、2.2×106 |
| B、2.2×105 |
| C、0.22×107 |
| D、22×105 |
 储油罐的截面如图所示,内径1000mm装入一些油后,若油面宽AB=600mm,求油的最大深度.
储油罐的截面如图所示,内径1000mm装入一些油后,若油面宽AB=600mm,求油的最大深度. 如图表示的是某种摩托车的油箱中剩余量y(升)与摩托车行驶路程x(千米)之间的关系.由图象可知,摩托车最多装
如图表示的是某种摩托车的油箱中剩余量y(升)与摩托车行驶路程x(千米)之间的关系.由图象可知,摩托车最多装 在如图所示的平面直角坐标系中,桥孔抛物线对应的二次函数关系式是y=-
在如图所示的平面直角坐标系中,桥孔抛物线对应的二次函数关系式是y=-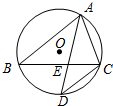 如图,⊙O是△ABC的外接圆,∠BAC的角平分线交BC于点E,交⊙O于点D,若AE=AC.求证:AB=AD.
如图,⊙O是△ABC的外接圆,∠BAC的角平分线交BC于点E,交⊙O于点D,若AE=AC.求证:AB=AD.