题目内容
当x 时,函数y=-
(x+3)2y随x的增大而增大,当x 时,随x的增大而减小.
| 1 |
| 2 |
考点:二次函数的性质
专题:
分析:利用二次函数的性质求解即可.
解答:解:∵函数y=-
(x+3)2的对称轴为x=-3,且开口向下,
∴当x<-3时,函数y=-
(x+3)2y随x的增大而增大,当x>-3时,随x的增大而减小.
故答案为:<-3,>-3.
| 1 |
| 2 |
∴当x<-3时,函数y=-
| 1 |
| 2 |
故答案为:<-3,>-3.
点评:本题主要考查了二次函数的性质,解题的关键是熟记二次函数的性质.

练习册系列答案
相关题目
下列图形中,一定相似的是( )
| A、两个矩形 |
| B、有一组角相等的两个等腰三角形 |
| C、有一组对应角相等的两个菱形 |
| D、两边对应成比例且有一组角相等的三角形 |
若二次函数y=x2-mx+1的图象的顶点在x轴上,则m的值是( )
| A、2 | B、-2 | C、0 | D、±2 |
关于函数y=3x2的性质的叙述,错误的是( )
| A、对称轴是y轴 |
| B、顶点是原点 |
| C、当x>0时,y随x的增大而增大 |
| D、y有最大值 |
已知x<0,且2x+|x|+3=0,则x=( )
| A、-1 | ||
| B、-2 | ||
C、-
| ||
| D、-3 |
有一应用题:“李老师存了一个两年的定期储蓄5000元,到期后扣除20%的利息税能取5176元,求这种储蓄的年利率是多少?”四位同学都是设这种储蓄的年利率是x,可他们列出的方程却不同,下列列出的方程中正确的是( )
| A、5000(1+x×2×20%)=5176 |
| B、5000(1+2x)×80%=5176 |
| C、5000+5000x×2×80%=5176 |
| D、5000+5000x×80%=5176 |
 如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO=
如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO=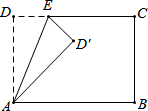 如图,矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿AE折叠,点D的对应点为D′.
如图,矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿AE折叠,点D的对应点为D′. 如图,在△ABC中,点D在BC上,AB=AC=CD,且AD=BD.求△ABC的三个内角.
如图,在△ABC中,点D在BC上,AB=AC=CD,且AD=BD.求△ABC的三个内角.