题目内容
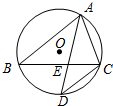 如图,⊙O是△ABC的外接圆,∠BAC的角平分线交BC于点E,交⊙O于点D,若AE=AC.求证:AB=AD.
如图,⊙O是△ABC的外接圆,∠BAC的角平分线交BC于点E,交⊙O于点D,若AE=AC.求证:AB=AD.考点:圆心角、弧、弦的关系,圆周角定理
专题:证明题
分析:利用角平分线的性质得出∠BAD=∠CAD,进而利用圆周角定理得出∠ABD=∠ADB,即可得出答案.
解答: 证明:连接BD,
证明:连接BD,
∵∠BAC的角平分线交BC于点E,交⊙O于点D,
∴∠BAD=∠CAD,
∵AE=AC,
∴∠AEC=∠ACE,
∵∠ACB=∠ADB,
∴∠AEC=∠ABD,
∴∠ABD=∠ADB,
∴AB=AD.
 证明:连接BD,
证明:连接BD,∵∠BAC的角平分线交BC于点E,交⊙O于点D,
∴∠BAD=∠CAD,
∵AE=AC,
∴∠AEC=∠ACE,
∵∠ACB=∠ADB,
∴∠AEC=∠ABD,
∴∠ABD=∠ADB,
∴AB=AD.
点评:此题主要考查了圆周角定理以及三角形内角和定理等知识,得出∠ABD=∠ADB是解题关键.

练习册系列答案
相关题目
下列图形中,一定相似的是( )
| A、两个矩形 |
| B、有一组角相等的两个等腰三角形 |
| C、有一组对应角相等的两个菱形 |
| D、两边对应成比例且有一组角相等的三角形 |
 请你根据图中所示写出一个乘法公式:
请你根据图中所示写出一个乘法公式: 如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO=
如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO=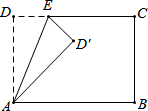 如图,矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿AE折叠,点D的对应点为D′.
如图,矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿AE折叠,点D的对应点为D′. 如图,在△ABC中,点D在BC上,AB=AC=CD,且AD=BD.求△ABC的三个内角.
如图,在△ABC中,点D在BC上,AB=AC=CD,且AD=BD.求△ABC的三个内角.