题目内容
4.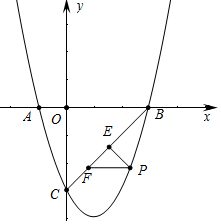 如图所示,抛物线y=ax2+bx-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
如图所示,抛物线y=ax2+bx-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.(1)求抛物线的解析式;
(2)如图所示,直线BC下方的抛物线上有一点D,过点D作DE⊥BC于点E,作DF平行于x轴交直线BC于点F,求△DEF周长的最大值;
(3)已知点M是抛物线的顶点,点N是y轴上一点,点Q是坐标平面内一点,若点P是抛物线上一点,且位于抛物线的对称轴右侧,是否存在以P、M、N、Q为顶点且以PM为边的正方形?若存在,直接写出点P的横坐标;若不存在,说明理由.
分析 (1)把A(-1,0),B(3,0)两点坐标代入抛物线y=ax2+bx-3,利用待定系数法即可解决问题;
(2)如图1中,连接PB、PC.设P(m,m2-2m-3),由题意△PEF是等腰直角三角形,PE最大时,△PEF的面积中点,此时△PBC的面积最大,则有S△PBC=S△POB+S△POC-S△BOC=$\frac{1}{2}$•3•(-m2+2m+3)+$\frac{1}{2}$•3•m-$\frac{9}{2}$=-$\frac{3}{2}$(m-$\frac{3}{2}$)2+$\frac{27}{8}$,易知m=$\frac{3}{2}$时,△PBC的面积最大,此时△PEF的面积也最大,由此求出PF的长即可解决问题.
(3)①当N与C重合时,点N关于对称轴的对称点P,此时思想MNQP是正方形,易知P(2,-3);②如图3中,当四边形PMQN是正方形时,作PF⊥y轴于N,ME∥x轴,PE∥y轴.易知△PFN≌△PEM,推出PF=PE,设P(m,m2-2m-3),M(1,-4),可得m=m2-2m-3-(-4),解方程即可解决问题;
解答 解:(1)把A(-1,0),B(3,0)两点坐标代入抛物线y=ax2+bx-3,
得到$\left\{\begin{array}{l}{a-b-3=0}\\{9a+3b-3=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$,
∴抛物线的解析式为y=x2-2x-3.
(2)如图1中,连接PB、PC.设P(m,m2-2m-3),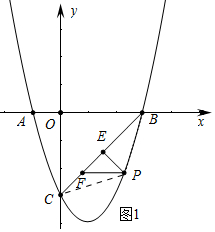
∵B(3,0),C(0,-3),
∴OB=OC,
∴∠OBC=45°,
∵PF∥OB,
∴∠PFE=∠OBC=45°,
∵PE⊥BC,
∴∠PEF=90°,
∴△PEF是等腰直角三角形,
∴PE最大时,△PEF的面积中点,此时△PBC的面积最大,
则有S△PBC=S△POB+S△POC-S△BOC=$\frac{1}{2}$•3•(-m2+2m+3)+$\frac{1}{2}$•3•m-$\frac{9}{2}$=-$\frac{3}{2}$(m-$\frac{3}{2}$)2+$\frac{27}{8}$,
∴m=$\frac{3}{2}$时,△PBC的面积最大,此时△PEF的面积也最大,
此时P($\frac{3}{2}$,-$\frac{15}{4}$),
∵直线BC的解析式为y=x-3,
∴F(-$\frac{3}{4}$,-$\frac{15}{4}$),
∴PF=$\frac{9}{4}$,
∵△PEF是等腰直角三角形,
∴EF=EP=$\frac{9\sqrt{2}}{8}$,
∴S△PEF最大值=$\frac{1}{2}$•$\frac{9\sqrt{2}}{8}$•$\frac{9\sqrt{2}}{8}$=$\frac{81}{64}$.
(3)①如图2中,
当N与C重合时,点N关于对称轴的对称点P,此时思想MNQP是正方形,易知P(2,-3).点P横坐标为2,
②如图3中,当四边形PMQN是正方形时,作PF⊥y轴于N,ME∥x轴,PE∥y轴.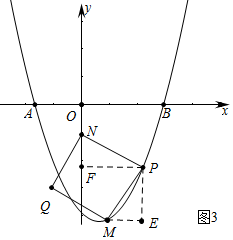
易知△PFN≌△PEM,
∴PF=PE,设P(m,m2-2m-3),
∵M(1,-4),
∴m=m2-2m-3-(-4),
∴m=$\frac{3+\sqrt{5}}{2}$或$\frac{3-\sqrt{5}}{2}$(舍弃),
∴P点横坐标为$\frac{3+\sqrt{5}}{2}$
所以满足条件的点P的横坐标为2或$\frac{3+\sqrt{5}}{2}$.
点评 本题考查二次函数的性质、一次函数、矩形的性质、对称等知识,解题的关键是添加常用辅助线构造全等三角形,学会构建二次函数解决最值问题,属于中考压轴题.

 如图:∠1与∠2互补,需要具备的条件是( )
如图:∠1与∠2互补,需要具备的条件是( )| A. | ∠1=∠3 | B. | ∠3+∠4=180° | C. | ∠3=∠4 | D. | ∠3+∠4=90° |
| A. | 205.5×104 | B. | 2.055×102 | C. | 2.055×1010 | D. | 2.055×1011 |
| A. | $\root{3}{64}$=4 | B. | $\sqrt{16}$=±4 | C. | $\sqrt{-9}$=3 | D. | $\sqrt{2\frac{1}{4}}$=$\frac{3}{4}$ |
 如图,在边长为8的正方形ABCD中,E是AB上的点,⊙O是以BC为直径的圆.
如图,在边长为8的正方形ABCD中,E是AB上的点,⊙O是以BC为直径的圆. 如图,已知AE∥BD,∠1=120°,∠2=32°,求∠C的度数.
如图,已知AE∥BD,∠1=120°,∠2=32°,求∠C的度数. 已知,如图,直线a∥b,则∠1、∠2、∠3、∠4之间的数量关系为∠1+∠4=∠2+∠3.
已知,如图,直线a∥b,则∠1、∠2、∠3、∠4之间的数量关系为∠1+∠4=∠2+∠3. 如图,若四边形ABCD是平行四边形,E、F分别是AB,AD边上的点,DE与CF交于点G,若E为AB的中点,AF=2FD,求$\frac{DG}{EG}+\frac{CG}{FG}$的值.
如图,若四边形ABCD是平行四边形,E、F分别是AB,AD边上的点,DE与CF交于点G,若E为AB的中点,AF=2FD,求$\frac{DG}{EG}+\frac{CG}{FG}$的值.