题目内容
4. 如图,若四边形ABCD是平行四边形,E、F分别是AB,AD边上的点,DE与CF交于点G,若E为AB的中点,AF=2FD,求$\frac{DG}{EG}+\frac{CG}{FG}$的值.
如图,若四边形ABCD是平行四边形,E、F分别是AB,AD边上的点,DE与CF交于点G,若E为AB的中点,AF=2FD,求$\frac{DG}{EG}+\frac{CG}{FG}$的值.
分析 延长DE交CB的延长线于M,根据平行四边形的性质得出AB∥CD,AD=BC,AD∥BC,推出△AED∽△BEM,△CMG∽△FDG,得出比例式,求出DE=ME,AD=BM=BC,$\frac{CG}{FG}$=$\frac{6DF}{DF}$=6,$\frac{DG}{EG}$=$\frac{1}{2}$,即可得出答案.
解答 解: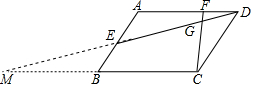
延长DE交CB的延长线于M,
∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC,AB=DC,AD∥BC,
∴△AED∽△BEM,
∴$\frac{AE}{BE}$=$\frac{AD}{BM}$=$\frac{DE}{ME}$,
∵E为AB中点,
∴AE=BE,
∴DE=ME,AD=BM=BC,
∵AD∥BC,
∴△CMG∽△FDG,
∴$\frac{CG}{FG}$=$\frac{CM}{DF}$=$\frac{GM}{DG}$,
∵AF=2DF,AD=BC=BM,
∴$\frac{CG}{FG}$=$\frac{6DF}{DF}$=6,
∴$\frac{GM}{DG}$=6,
∴$\frac{DE}{DG}$=3,
∴$\frac{DG}{EG}$=$\frac{1}{2}$,
∴$\frac{DG}{EG}+\frac{CG}{FG}$=$\frac{1}{2}$+6=$\frac{13}{2}$.
点评 本题考查了平行四边形的性质和相似三角形的性质和判定,能灵活运用相似三角形的性质得出正确的比例式是解此题的关键.

练习册系列答案
相关题目
3.下列式子正确的是( )
| A. | $\root{3}{-6}=-\root{3}{6}$ | B. | $±\sqrt{16}=4$ | C. | $\sqrt{25}$=±5 | D. | $\sqrt{(-3)^{2}}$=-3 |
8.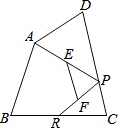 如图,已知四边形ABCD中,R,P分别是BC,CD边上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,下列结论成立的是( )
如图,已知四边形ABCD中,R,P分别是BC,CD边上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,下列结论成立的是( )
 如图,已知四边形ABCD中,R,P分别是BC,CD边上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,下列结论成立的是( )
如图,已知四边形ABCD中,R,P分别是BC,CD边上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,下列结论成立的是( )| A. | △EFP的周长不变 | B. | 线段EF的长与点P的位置无关 | ||
| C. | 点P到EF的距离不变 | D. | ∠APR的大小不变 |
13.关于$\sqrt{12}$的叙述,错误的是( )
| A. | $\sqrt{12}$是有理数 | B. | 面积为12的正方形边长是$\sqrt{12}$ | ||
| C. | $\sqrt{12}$是12的算术平方根 | D. | 在数轴上可以找到表示$\sqrt{12}$的点 |
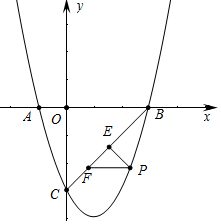 如图所示,抛物线y=ax2+bx-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
如图所示,抛物线y=ax2+bx-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C. 如图,直线AB、CD相交于O点,∠AOC=80°,OE⊥AB,OF平分∠DOB,求∠EOF的度数.
如图,直线AB、CD相交于O点,∠AOC=80°,OE⊥AB,OF平分∠DOB,求∠EOF的度数.