题目内容
1．化简$\frac{1}{{\sqrt{3}-1}}-\frac{1}{{\sqrt{3}+1}}$的值是（ ）| A． | 1 | B． | -1 | C． | $\sqrt{3}$ | D． | $-\sqrt{3}$ |
分析 先分母有理化，然后合并即可．
解答 解：原式=$\frac{\sqrt{3}+1}{2}$-$\frac{\sqrt{3}-1}{2}$
=1．
故选A．
点评 本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．
练习册系列答案
相关题目
16．若-1＜a＜0，则a、$\frac{1}{a}$、a2按从小到大的顺序排列为（ ）
| A． | $a＜\frac{1}{a}＜{a^2}$ | B． | $\frac{1}{a}＜a＜{a^2}$ | C． | $a＜{a^2}＜\frac{1}{a}$ | D． | ${a^2}＜a＜\frac{1}{a}$ |
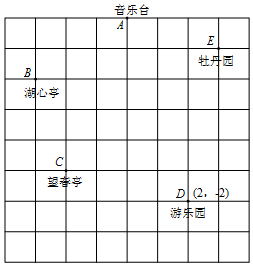小王到公园游玩，回到家后，她利用平面直角坐标系画出了公园的景区地图，如图所示，可是她忘记了在图中标出原点和x轴、y轴，只知道游乐园D的坐标为（2，-2），且一格表示一个单位长度．
13．
在如图所示的正方形纸片上做随机扎针实验，则针头扎在阴影区域内的概率为（ ）
在如图所示的正方形纸片上做随机扎针实验，则针头扎在阴影区域内的概率为（ ）| A． | 0.25 | B． | 0.5 | C． | 0.125 | D． | 0.1 |
