题目内容
E为正方形ABCD的边BC上一点，BE=3cm，EC=1cm，DF⊥AE交AE于点F，求DF的长．考点：正方形的性质,勾股定理
专题：
分析：可先证明△ABE∽△DFA，由条件可求得AB、AD，结合相似三角形的性质可求得DF．
解答：解：∵四边形ABCD为正方形，
∴AB=AD=BC=BE+CE=4cm，∠B=∠DAB=90°，
∵DF⊥AE，
∴∠DFA=∠B=90°，且∠DAF+∠BAF=∠BAF+∠BEA=90°，
∴∠DAF=∠BEA，
∴△ABE∽△DFA，
∴
=
，
在Rt△ABE中，由勾股定理可求得AE=5cm，
∴
=
，
∴DF=
cm．
∴AB=AD=BC=BE+CE=4cm，∠B=∠DAB=90°，
∵DF⊥AE，
∴∠DFA=∠B=90°，且∠DAF+∠BAF=∠BAF+∠BEA=90°，
∴∠DAF=∠BEA，
∴△ABE∽△DFA，
∴
| AB |
| DF |
| AE |
| AD |
在Rt△ABE中，由勾股定理可求得AE=5cm，
∴
| 4 |
| DF |
| 5 |
| 4 |
∴DF=
| 16 |
| 5 |
点评：本题主要考查正方形的性质，由正方形的性质证明△ABE∽△DFA是解题的关键．
练习册系列答案
相关题目
如图，在?ABCD中，∠DBC=45°，DE⊥BC于E，BF⊥CD于F，DE、BF 相交于H，BF、AD的延长线相交于G，下面结论：①BD=
先作图，再证明．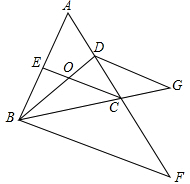
如图，△ABC中，∠ABC=∠ACB，BD平分∠ABC，CE平分∠ACB，BD，CE交于点O，F，G分别是AC，BC延长线上一点，且∠EOD+∠OBF=180°，∠DBC=∠G，指出图中所有平行线，并说明理由．
看图写出下列各点坐标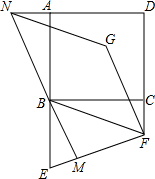
如图，已知正方形ABCD，E是AB延长线上一点，F是DC延长线上一点，连接BF、EF，恰有BF=EF，将线段EF绕点F顺时针旋转90°得FG，过点B作EF的垂线，交EF于点M，交DA的延长线于点N，连接NG．
如图，AB是半圆O的直径，D，E是半圆上任意两点，连结AD，DE，AE与BD相交于点C，要使△ADC与△ABD相似，可以添加一个条件．下列添加的条件其中错误的是（ ）| A、∠ACD=∠DAB |
| B、AD=DE |
| C、AD2=BD•CD |
| D、AD•AB=AC•BD |
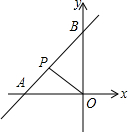如图已知直线y=