题目内容
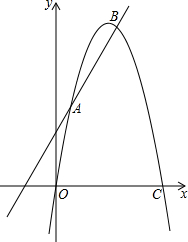 如图所示,已知抛物线y=ax2+bx+c与直线y=kx+4相交于A(1,5),B(4,8)两点,与x轴交于原点O及C点.
如图所示,已知抛物线y=ax2+bx+c与直线y=kx+4相交于A(1,5),B(4,8)两点,与x轴交于原点O及C点.(1)求直线和抛物线的解析式;
(2)在x轴上方的抛物线上是否存在点D,使得S△OCD=
| 1 |
| 2 |
考点:待定系数法求二次函数解析式,待定系数法求一次函数解析式,二次函数图象上点的坐标特征
专题:计算题
分析:(1)设直线解析式为y=mx+n,把A与B坐标代入求出m与n的值,确定出直线解析式;把A与B,原点O坐标代入抛物线解析式求出a,b,c的值,即可确定出抛物线解析式;
(2)求出三角形OCB的面积,设D的纵坐标为y,表示出三角形OCD面积,根据两三角形面积关系求出y的值,确定出D坐标即可.
(2)求出三角形OCB的面积,设D的纵坐标为y,表示出三角形OCD面积,根据两三角形面积关系求出y的值,确定出D坐标即可.
解答: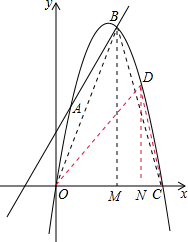 解:(1)设直线AB解析式为y=mx+n,
解:(1)设直线AB解析式为y=mx+n,
把A(1,5),B(4,8)代入得:
,
解得:m=1,n=4,
∴直线解析式为y=x+4;
把A(1,5),B(4,8)以及O(0,0)代入抛物线解析式得:
,
解得:a=-1,b=6,c=0,
则抛物线解析式为y=-x2+6x;
(2)过B作BM⊥x轴,交x轴于点M,设D纵坐标为y,
令抛物线解析式y=0,得到x=0或x=6,即C(6,0),O(0,0),
∴S△BOC=
OC•BM=24;
∵S△OCD=
S△OCB=12,
∴
OC•|DN|=12,即|DN|=4,
解得:DN=4或-4,即y=4或-4,
当y=4时,4=-x2+6x,
解得:x=3±
,此时D(3+
,4)或(3-
,4);
当y=-4时,-4=-x2+6x,
解得:x=3±
,此时D(3+
,-4)或(3+
,-4).
 解:(1)设直线AB解析式为y=mx+n,
解:(1)设直线AB解析式为y=mx+n,把A(1,5),B(4,8)代入得:
|
解得:m=1,n=4,
∴直线解析式为y=x+4;
把A(1,5),B(4,8)以及O(0,0)代入抛物线解析式得:
|
解得:a=-1,b=6,c=0,
则抛物线解析式为y=-x2+6x;
(2)过B作BM⊥x轴,交x轴于点M,设D纵坐标为y,
令抛物线解析式y=0,得到x=0或x=6,即C(6,0),O(0,0),
∴S△BOC=
| 1 |
| 2 |
∵S△OCD=
| 1 |
| 2 |
∴
| 1 |
| 2 |
解得:DN=4或-4,即y=4或-4,
当y=4时,4=-x2+6x,
解得:x=3±
| 5 |
| 5 |
| 5 |
当y=-4时,-4=-x2+6x,
解得:x=3±
| 13 |
| 13 |
| 13 |
点评:此题考查了待定系数法求抛物线解析式,待定系数法求一次函数解析式,以及二次函数图象上点的特征,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如图,△ABC内接于⊙O,∠C=45°,AB=8,则⊙O的半径为( )
如图,△ABC内接于⊙O,∠C=45°,AB=8,则⊙O的半径为( )A、4
| ||
| B、8 | ||
C、4
| ||
| D、9 |
某校科技制作小组有4名女生和6名男生,现从中任选1人去参加市科技制作比赛,则选中女生的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
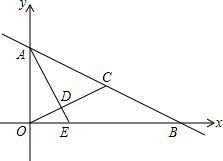 如图,在平面直角坐标系中,点A在y轴上,点B在x轴上,C是线段AB的中点,连接OC,并过点A作OC的垂线,垂足为D,交x轴于点E,已知tan∠OAD=
如图,在平面直角坐标系中,点A在y轴上,点B在x轴上,C是线段AB的中点,连接OC,并过点A作OC的垂线,垂足为D,交x轴于点E,已知tan∠OAD=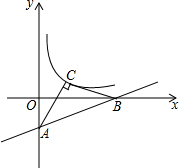 已知:如图,直线y=
已知:如图,直线y= 如图所示,直角三角尺放在一条直线上,求∠1+∠2的度数.
如图所示,直角三角尺放在一条直线上,求∠1+∠2的度数. 如图,在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF 相交于H,BF、AD的延长线相交于G,下面结论:①BD=
如图,在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF 相交于H,BF、AD的延长线相交于G,下面结论:①BD= 如图,在Rt△ABC中,∠C=90°,AC=4,cosA=
如图,在Rt△ABC中,∠C=90°,AC=4,cosA= 看图写出下列各点坐标
看图写出下列各点坐标