题目内容
4. 如图,王大伯家屋后有一块长12m、宽8m的长方形空地,他在以较长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长最长不超过( )
如图,王大伯家屋后有一块长12m、宽8m的长方形空地,他在以较长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长最长不超过( )| A. | 3m | B. | 4m | C. | 5m | D. | 6m |
分析 为了不让羊吃到菜,必须≤点A到圆的最小距离.要确定最小距离,连接OA交半圆于点E,即AE是最短距离.在直角三角形AOB中,因为OB=6m,BA=8m,所以根据勾股定理得OA=10m.那么AE的长即可解答.
解答  解:连接OA,交⊙O于E点,
解:连接OA,交⊙O于E点,
在Rt△OAB中,OB=6m,BA=8m,
所以OA=$\sqrt{B{O}^{2}+A{B}^{2}}$=10m;
又因为OE=OB=6m,
所以AE=OA-OE=4m.
因此拴羊的绳长最长不超过4m.
故选:B.
点评 此题考查了点与圆的位置关系,此题确定点到半圆的最短距离是难点.熟练运用勾股定理.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
4.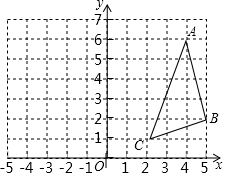 如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90°,得到△A′B′C,那么点A、B的对应点A′、B′的坐标分别是( )
如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90°,得到△A′B′C,那么点A、B的对应点A′、B′的坐标分别是( )
 如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90°,得到△A′B′C,那么点A、B的对应点A′、B′的坐标分别是( )
如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90°,得到△A′B′C,那么点A、B的对应点A′、B′的坐标分别是( )| A. | (-3,3)、(-2,4) | B. | (3,-3)、(1,4) | C. | (3,-3)、(-2,4) | D. | (-3,3)、(1,4) |
1.某市出租车的收费标准是:起步价8元(即行驶距离不超过3千米都需付8元车费),超过3千米以后,每增加1千米,加收2.6元(不足1千米按1千米计),某人从甲地到乙地经过的路程是x千米,出租车费为21元,那么x的最大值是( )
| A. | 11 | B. | 8 | C. | 7 | D. | 5 |
9.下列各式的变形中,正确的是( )
| A. | x6÷x=x | B. | (x2-$\frac{1}{x}$)÷x=x-1 | C. | x2+x3=x5 | D. | x2-x+1=(x-$\frac{1}{2}$)2+$\frac{3}{4}$ |
 如图,在?ABCD中,E,F是对角线BD上的点,且BE=DF,求证:四边形AECF是平行四边形.
如图,在?ABCD中,E,F是对角线BD上的点,且BE=DF,求证:四边形AECF是平行四边形.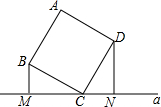 如图,正方形ABCD的顶点C在直线a上,且点B,D到a的距离分别是1,2.则这个正方形的面积是5.
如图,正方形ABCD的顶点C在直线a上,且点B,D到a的距离分别是1,2.则这个正方形的面积是5.