题目内容
14.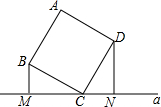 如图,正方形ABCD的顶点C在直线a上,且点B,D到a的距离分别是1,2.则这个正方形的面积是5.
如图,正方形ABCD的顶点C在直线a上,且点B,D到a的距离分别是1,2.则这个正方形的面积是5.
分析 根据正方形的性质可得BC=CD,∠BCD=90°,然后求出∠BCM=∠CDN,再利用“角角边”证明△BCM和△CDN全等,根据全等三角形对应边相等可得CM=DN,再利用勾股定理可得BC2=BM2+CM2,然后根据正方形的面积求解即可.
解答 解:在正方形ABCD中,BC=CD,∠BCD=90°,
∴∠BCM+∠DCN=90°
∵BM⊥a,DN⊥a,
∴∠BMC=∠CND=90°,
∴∠CDN+∠DCN=90°,
∴∠BCM=∠CDN,
在△BCM和△CDN中,$\left\{\begin{array}{l}{∠BCM=∠CDN}\\{∠BMC=∠CND=90°}\\{BC=CD}\end{array}\right.$,
∴△BCM≌△CDN(AAS),
∴CM=DN,
在Rt△BCM中,根据勾股定理得,BC2=BM2+CM2,
∴BC2=BM2+DN2,
∵BM=1,DN=2,正方形的面积=BC2,
∴这个正方形的面积=12+22=1+4=5.
故答案为:5.
点评 本题考查了正方形的性质,全等三角形的判定与性质,熟练掌握正方形的性质以及三角形全等的判定方法是解题的关键,此类题目,根据同角的余角相等求出相等的锐角是难点.

练习册系列答案
相关题目
4. 如图,王大伯家屋后有一块长12m、宽8m的长方形空地,他在以较长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长最长不超过( )
如图,王大伯家屋后有一块长12m、宽8m的长方形空地,他在以较长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长最长不超过( )
 如图,王大伯家屋后有一块长12m、宽8m的长方形空地,他在以较长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长最长不超过( )
如图,王大伯家屋后有一块长12m、宽8m的长方形空地,他在以较长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长最长不超过( )| A. | 3m | B. | 4m | C. | 5m | D. | 6m |
2.若抛物线y=x2-2x-1与x轴的一个交点坐标为(m,0),则代数式m2-2m+2017的值为( )
| A. | 2019 | B. | 2018 | C. | 2016 | D. | 2015 |
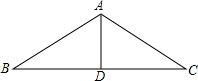 如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10m,中柱AD(D为BC中点)的长是3.6m,则∠BAC=108°(用科学计算器计算,结果精确到1°).
如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10m,中柱AD(D为BC中点)的长是3.6m,则∠BAC=108°(用科学计算器计算,结果精确到1°).