题目内容
19.将一副直角三角板如图1摆放在直线AD上(直角三角板OBC和直角三角板MON,∠OBC=90°,∠BOC=45°,∠MON=90°,∠MNO=30°),保持三角板OBC不动,将三角板MON绕点O以每秒10°的速度顺时针旋转直至ON边第一次重合在直线AD上,整个过程时间记为t秒.
(1)从旋转开始至结束,整个过程共持续了9秒;
(2)如图2,旋转三角板MON,使得OM、ON在直线OC的异侧,请直接写出∠CON与∠AOM数量关系;
如图3,继续旋转三角板MON,使得OM、ON同时在直线OC的右侧,请问上面的数量关系是否仍然成立?并说明理由.
(3)若在三角板MON旋转的同时,另一个三角板OBC也绕点O以每秒12°的速度顺时针旋转,当ON边第一次重合在直线AD上时两三角板同时停止.
①试用字母t分别表示∠AOM与∠AOC;
②在旋转的过程中,当t为何值时OM平分∠AOC.
分析 (1)根据∠NOD=90°即可解决问题;
(2)①结论:∠CON-∠AOM=45°;由∠CON=90°-∠COM,∠AON=45°-∠COM,可得∠CON-∠AOM=(90°-∠COM)-(45°-∠COM)=45°
②如图3中,结论仍然成立.证明方法类似;
(3)①∠AOM=10°t,∠AOC=12°t+45°;
②由OM平分∠AOC,可得∠AOC=2∠AOM,由此列出方程12°t+45°=2•10°t,即可解决问题;
解答 解:(1)如图1中,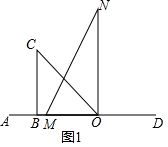
∵∠MON=∠NOD=90°,
∴t=$\frac{90}{10}$=9s.
故答案为9.
(2)①结论:∠CON-∠AOM=45°;
理由:如图2中,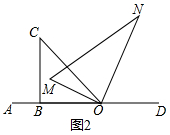
∵∠CON=90°-∠COM,∠AON=45°-∠COM,
∴∠CON-∠AOM=(90°-∠COM)-(45°-∠COM)=45°
②如图3中,结论仍然成立.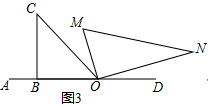
理由:∵∠CON=90°+∠COM,∠AOM=45°+∠COM,
∴∠CON-∠AOM=(90°+∠COM)-(45°+∠COM)=45°.
(3)①∠AOM=10t,∠AOC=12t+45;
②∵OM平分∠AOC,
∴∠AOC=2∠AOM,
∴12t+45°=2×10t,
解得:t=$\frac{45}{8}$,
∴当t为$\frac{45}{8}$s时OM平分∠AOC.
点评 本题考查三角形综合题、直角三角形的性质、角平分线的性质等知识,解题的关键是灵活运用所学知识解决问题,学会用构建方程的思想思考问题,属于中考常考题型.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
7.在平面直角坐标系中,将点A先向左平移3个单位,再向下平移2个单位,得到点B(-2,1),则点A的坐标为( )
| A. | (-5,3) | B. | (-5,-1) | C. | (1,3) | D. | (1,-3) |
4.把直线y=-5x+3向上平移m个单位后,与直线y=2x+4的交点在第一象限,则m的取值范围是( )
| A. | m<4 | B. | m>1 | C. | 1<m<7 | D. | 3<m<4 |
11.若关于x的不等式ax-b>0的解集为x<$\frac{1}{3}$,则关于x的不等式(a+b)x>a-b的解集为( )
| A. | x<-$\frac{1}{2}$ | B. | x$>-\frac{1}{2}$ | C. | x$<\frac{1}{2}$ | D. | x$>\frac{1}{2}$ |
8.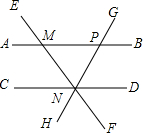 如图,直线AB∥CD,直线EF分别交AB,CD于点M,N,过点N的直线GH交AB于点P,下列结论错误的是( )
如图,直线AB∥CD,直线EF分别交AB,CD于点M,N,过点N的直线GH交AB于点P,下列结论错误的是( )
 如图,直线AB∥CD,直线EF分别交AB,CD于点M,N,过点N的直线GH交AB于点P,下列结论错误的是( )
如图,直线AB∥CD,直线EF分别交AB,CD于点M,N,过点N的直线GH交AB于点P,下列结论错误的是( )| A. | ∠DNG=∠AME | B. | ∠BMN=∠MNC | C. | ∠CNH=∠BPG | D. | ∠EMB=∠END |
 如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.