题目内容
已知x=
+
,y=
-
,求下列各式的值:
(1)x2+y2;
(2)x2-xy+y2;
(3)
+
.
| 1 | ||
|
| 4 |
| 1 | ||
|
| 4 |
(1)x2+y2;
(2)x2-xy+y2;
(3)
| 1 |
| x |
| 1 |
| y |
考点:二次根式的化简求值
专题:计算题
分析:计算出x+y=
,xy=-
,
(1)把x2+y2变形为(x+y)2-2xy,然后利用整体代入的方法计算;
(2)把原式变形为原式=(x+y)2-3xy,然后利用整体代入的方法计算;
(3)先通分,然后利用整体代入的方法计算.
2
| ||
| 5 |
| 19 |
| 5 |
(1)把x2+y2变形为(x+y)2-2xy,然后利用整体代入的方法计算;
(2)把原式变形为原式=(x+y)2-3xy,然后利用整体代入的方法计算;
(3)先通分,然后利用整体代入的方法计算.
解答:解:∵x=
+
,y=
-
,
∴x+y=
=
,xy=
-4=-
,
(1)原式=(x+y)2-2xy=(
)2-2×(-
)=
;
(2)原式=(x+y)2-3xy=(
)2-3×(-
)=
;
(3)原式=
=-
.
| 1 | ||
|
| 4 |
| 1 | ||
|
| 4 |
∴x+y=
| 2 | ||
|
2
| ||
| 5 |
| 1 |
| 5 |
| 19 |
| 5 |
(1)原式=(x+y)2-2xy=(
2
| ||
| 5 |
| 19 |
| 5 |
| 42 |
| 5 |
(2)原式=(x+y)2-3xy=(
2
| ||
| 5 |
| 19 |
| 5 |
| 61 |
| 5 |
(3)原式=
| x+y |
| xy |
2
| ||
| 19 |
点评:本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.

练习册系列答案
相关题目
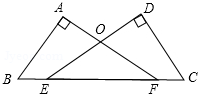 已知:如图,E是BC的中点,∠1=∠2,∠B=∠C.求证:AB=DC.
已知:如图,E是BC的中点,∠1=∠2,∠B=∠C.求证:AB=DC.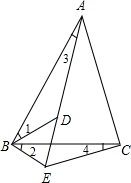 如图,D为△ABC内一点,E为△ABC外一点,且∠1=∠2,∠3=∠4.
如图,D为△ABC内一点,E为△ABC外一点,且∠1=∠2,∠3=∠4.