题目内容
20.在1个不透明的口袋里,装有红、白、黄三种颜色的乒乓球(除颜色外,其余都相同),其中有白球2个,黄球1个,若从中任意摸出一个球,这个球是白色的概率为$\frac{1}{2}$.(1)求口袋中红球的个数;
(2)若摸到红球记0分,摸到白球记1分,摸到黄球记2分.甲从口袋中摸出一个球,不放回,再摸出一个,请用画树状图或列表的方法求甲摸出两个球得2分的概率.
分析 (1)首先设红球有x个,由概率公式可得$\frac{2}{2+1+x}$,解此方程即可求得答案;
(2)首先根据题意列出表格,然后由表格即可求得所有等可能的结果与摸出两个球得2分的情况,再利用概率公式求解即可求得答案.
解答 解:(1)设红球有x个,
则$\frac{2}{2+1+x}$=0.5,
解得:x=1,
经检验:x=1是原分式方程的解;
∴红球有1个;
(2)列表如下:
| 红 | 白1 | 白2 | 黄 | |
| 红 | (红,红) | (红,白1) | (红,白2) | (红,黄) |
| 白1 | (白1,红) | (白1,白1) | (白1,白2) | (白1,黄) |
| 白2 | (白2,红) | (白2,白1) | (白2,白2) | (白2,黄) |
| 黄 | (黄,红) | (黄,白1) | (黄,白2) | (黄,黄) |
∴P(摸出两个球得2分)=$\frac{6}{16}=\frac{3}{8}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
11.四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
| A. | AB=CD | B. | AD=BC | C. | AB=BC | D. | AC=BD |
11.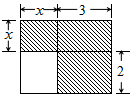 下面四个整式中,不能表示图中阴影部分面积的是( )
下面四个整式中,不能表示图中阴影部分面积的是( )
 下面四个整式中,不能表示图中阴影部分面积的是( )
下面四个整式中,不能表示图中阴影部分面积的是( )| A. | (x+3)(x+2)-2x | B. | x(x+3)+6 | C. | 3(x+2)+x2 | D. | x2+5x |
8.下列调查中,适宜采用全面调查方式的是( )
| A. | 了解一批圆珠笔的使用寿命 | |
| B. | 了解全国八年级学生身高的现状 | |
| C. | 检查发射神舟11号飞船的运载火箭的各零部件 | |
| D. | 考察世界人们保护海洋的意识 |
9.将抛物线y=2x2向右平移1个单位,再向下平移2个单位后得到的抛物线的解析式为( )
| A. | y=2(x+1)2-2 | B. | y=2(x-1)2-2 | C. | y=2(x-2)2-1 | D. | y=2(x+2)2+1 |
 如图,⊙O的直径AB垂直于弦CD,垂足为P,BP=2cm,CD=6cm,求直径AB的长.
如图,⊙O的直径AB垂直于弦CD,垂足为P,BP=2cm,CD=6cm,求直径AB的长.