题目内容
15. 如图,⊙O的直径AB垂直于弦CD,垂足为P,BP=2cm,CD=6cm,求直径AB的长.
如图,⊙O的直径AB垂直于弦CD,垂足为P,BP=2cm,CD=6cm,求直径AB的长.
分析 连接OC,由 垂径定理可知CP=$\frac{1}{2}$CD=3,设半径为r,由勾股定理可求出r的值.
解答 解:连接OC ∵OB⊥CD,O为圆心
∵OB⊥CD,O为圆心
∴CP=$\frac{1}{2}$CD=3,
设OC=OB=r,
∴OP=r-2,
在Rt△OCP中,由勾股定理得:
(r-2)2+32=r2,
∴r=$\frac{13}{4}$
∴直径AB=2r=$\frac{13}{2}$
点评 本题考查垂径定理,涉及勾股定理,一元一次方程的解法,完全平方公式,解题的关键是根据勾股定理列出方程求出r的值.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
7.下面的图形是由边长为1的正方形按照某种规律排列而组成的.
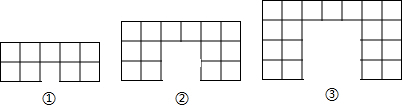
(1)观察图形,填写下表:
(2)推测第n个图形中,正方形的个数为5n+3,周长为10n+8(都用含n的代数式表示).
(3)写出第2016个图形的周长.

(1)观察图形,填写下表:
| 图形个数(n) | ① | ② | ③ |
| 正方形的个数 | 9 | 13 | 18 |
| 图形的周长 | 16 | 28 | 38 |
(3)写出第2016个图形的周长.