题目内容
20.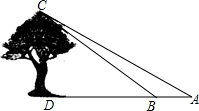 大庄中学9年级学生在学习“解直角三角形”一章时,开展测量物体高度的实践活动,他们要测量校园内一棵大树的高度.如图,在大树前的平地上选一点A,测得由点A看大树顶端C的仰角为35°,在点A和大树之间选择一点B(A,B,D在同一直线上),测得由点B看大树顶端C的仰角为45°,再量得A,B两点间的距离为5.43米,求大树CD的高度(结果精确到0.1米).(测角器的高度忽略不计.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin45°≈0.71,cos45°≈0.71)
大庄中学9年级学生在学习“解直角三角形”一章时,开展测量物体高度的实践活动,他们要测量校园内一棵大树的高度.如图,在大树前的平地上选一点A,测得由点A看大树顶端C的仰角为35°,在点A和大树之间选择一点B(A,B,D在同一直线上),测得由点B看大树顶端C的仰角为45°,再量得A,B两点间的距离为5.43米,求大树CD的高度(结果精确到0.1米).(测角器的高度忽略不计.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin45°≈0.71,cos45°≈0.71)
分析 设树的高度为x米,分别在Rt△ACD和Rt△BCD中,表示出AD、BD的长度,然后根据A,B两点间的距离为5.43米,列出方程,求出x的值.
解答 解:设树的高度为x米,
在Rt△ACD中,
∵∠A=35°,CD=x,
∴AD=$\frac{CD}{tan35°}$=$\frac{x}{0.7}$.
在Rt△BCD中,
∵∠CBD=45°,
∴BD=CD=x,
∵AB=5.43,
∴$\frac{x}{0.7}$-x=5.43,
解得:x=12.67≈12.7.
答:大树CD的高度约为12.7米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据俯角构造直角三角形,利用三角函数的知识求解,难度一般.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 某校数学兴趣小组用高为1.5米的仪器测量建筑物CD的高度,如图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为β,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为α,测得A、B之间的距离为2米,tanα=$\frac{6}{5}$,tanβ=$\frac{10}{9}$,试求建筑物CD的高度.
某校数学兴趣小组用高为1.5米的仪器测量建筑物CD的高度,如图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为β,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为α,测得A、B之间的距离为2米,tanα=$\frac{6}{5}$,tanβ=$\frac{10}{9}$,试求建筑物CD的高度. 如图:已知AB=CD,AB∥CD,试说明△ABO≌△DCO.
如图:已知AB=CD,AB∥CD,试说明△ABO≌△DCO. AB是圆O的直径,点C,D都在圆O上,连接CA,CB,DC,DB.已知∠D=30°,BC=3,则AC的长是3$\sqrt{3}$.
AB是圆O的直径,点C,D都在圆O上,连接CA,CB,DC,DB.已知∠D=30°,BC=3,则AC的长是3$\sqrt{3}$. 如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=4,DE垂直平分斜边AC,交AB于D,E为垂足,连接CD,则AD的长为( )
如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=4,DE垂直平分斜边AC,交AB于D,E为垂足,连接CD,则AD的长为( )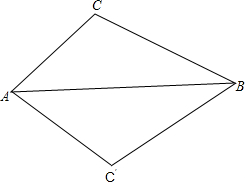 如图所示,把上边的图形沿AB翻折后得到下边的图形,则有三对角对应相等,这三对角分别为∠C=∠C′,∠CAB=∠C′AB,∠CBA=∠C′BA.
如图所示,把上边的图形沿AB翻折后得到下边的图形,则有三对角对应相等,这三对角分别为∠C=∠C′,∠CAB=∠C′AB,∠CBA=∠C′BA.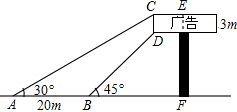 如图,某广告牌竖直矗立在水平地面上,经测量得到如下相关数据:CD=3m,AB=20m,∠CAB=30°,∠DBF=45°,求广告牌的高EF(结果保留根号).
如图,某广告牌竖直矗立在水平地面上,经测量得到如下相关数据:CD=3m,AB=20m,∠CAB=30°,∠DBF=45°,求广告牌的高EF(结果保留根号).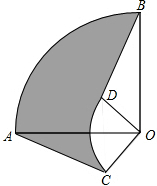 如图,圆心角都是90°的扇形AOB与扇形COD如图叠放在一起,连结AC、BD,若OA=3cm,OC=1cm,则阴影部分的面积为2π平方厘米.
如图,圆心角都是90°的扇形AOB与扇形COD如图叠放在一起,连结AC、BD,若OA=3cm,OC=1cm,则阴影部分的面积为2π平方厘米.