题目内容
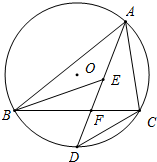 如图,已知△ABC内接于⊙O,AD平分∠BAC交BC于点F,交⊙O于点D,E是△ABC内心,连BE.
如图,已知△ABC内接于⊙O,AD平分∠BAC交BC于点F,交⊙O于点D,E是△ABC内心,连BE.(1)求证:ED=DC;
(2)若∠BAC=60°,AB=11,AC=7,求AD的长.
考点:三角形的内切圆与内心
专题:证明题
分析:(1)如图1,由AD平分∠BAC交⊙O于D得∠1=∠2,根据圆周角定理得
=
,则BD=CD,再利用E是△ABC内心得∠3=∠4,然后证明∠BED=∠DBE,根据等腰三角形的判定得到BD=ED,即ED=DC;
(2)作CQ⊥AB于Q,连结OB,连结OD交BC于H,如图2,在Rt△ACQ中根据含30度的直角三角形三边的关系得AQ=
,CQ=
,则BQ=AB-AQ=
;在Rt△BCQ中,根据勾股定理计算出BC=2
,根据垂径定理的推论,由
=
得OD⊥BC,BH=CH=
BC=
,再证明△OBD为等边三角形,计算出OH=
,OB=2
,BD=2
,DH=
;接着根据角平分线定理得到
=
,可计算出BF=
,则HF=BF-BH=
,然后在Rt△DHF中,利用勾股定理计算出DF=
,最后证明△DBF∽△DAB,利用相似比计算出AD.
 |
| BD |
 |
| CD |
(2)作CQ⊥AB于Q,连结OB,连结OD交BC于H,如图2,在Rt△ACQ中根据含30度的直角三角形三边的关系得AQ=
| 7 |
| 2 |
7
| ||
| 2 |
| 15 |
| 2 |
| 93 |
 |
| BD |
 |
| CD |
| 1 |
| 2 |
| 93 |
| 31 |
| 31 |
| 31 |
| 31 |
| BF |
| CF |
| AB |
| AC |
11
| ||
| 9 |
2
| ||
| 9 |
31
| ||
| 9 |
解答:(1)证明:如图1,
∵AD平分∠BAC交⊙O于D,
∴∠1=∠2,
∴
=
,
∴BD=CD,
∵E是△ABC内心,
∴BE平分∠ABC,
∴∠3=∠4,
∵∠BED=∠1+∠3,
∵∠1=∠5,
∴∠DBE=∠4+∠5,
即∠BED=∠DBE,
∴BD=ED,
∴ED=DC;
(2)解:作CQ⊥AB于Q,连结OB,连结OD交BC于H,如图2,
在Rt△ACQ中,∵∠CAQ=60°,AC=7,
∴AQ=
,CQ=
,
∴BQ=AB-AQ=
,
在Rt△BCQ中,BC=
=2
,
∵
=
,
∴OD⊥BC,
∴BH=CH=
BC=
,
∵AD平分∠BAC,
∴∠BAD=
∠BAC=30°,
∴∠BOD=2∠BAD=60°,
∴△OBD为等边三角形,
在Rt△OBH中,OH=
BH=
,
∴OB=2OH=2
,
∴BD=2
,DH=
,
∵AD平分∠BAC,
∴
=
=
,即
=
,
∴BF=
BC=
•2
=
,
∴HF=BF-BH=
,
在Rt△DHF中,DF=
=
,
∵∠DBF=∠DAB,∠FDB=∠BDA,
∴△DBF∽△DAB,
∴DF:BD=BD:AD,即
:2
=2
:AD,
∴AD=12
.

∵AD平分∠BAC交⊙O于D,
∴∠1=∠2,
∴
 |
| BD |
 |
| CD |
∴BD=CD,
∵E是△ABC内心,
∴BE平分∠ABC,
∴∠3=∠4,
∵∠BED=∠1+∠3,
∵∠1=∠5,
∴∠DBE=∠4+∠5,
即∠BED=∠DBE,
∴BD=ED,
∴ED=DC;
(2)解:作CQ⊥AB于Q,连结OB,连结OD交BC于H,如图2,
在Rt△ACQ中,∵∠CAQ=60°,AC=7,
∴AQ=
| 7 |
| 2 |
7
| ||
| 2 |
∴BQ=AB-AQ=
| 15 |
| 2 |
在Rt△BCQ中,BC=
| CQ2+BQ2 |
| 93 |

∵
 |
| BD |
 |
| CD |
∴OD⊥BC,
∴BH=CH=
| 1 |
| 2 |
| 93 |
∵AD平分∠BAC,
∴∠BAD=
| 1 |
| 2 |
∴∠BOD=2∠BAD=60°,
∴△OBD为等边三角形,
在Rt△OBH中,OH=
| ||
| 3 |
| 31 |
∴OB=2OH=2
| 31 |
∴BD=2
| 31 |
| 31 |
∵AD平分∠BAC,
∴
| BF |
| CF |
| AB |
| AC |
| 11 |
| 7 |
| BF |
| BF+CF |
| 11 |
| 11+7 |
∴BF=
| 11 |
| 18 |
| 11 |
| 18 |
| 93 |
11
| ||
| 9 |
∴HF=BF-BH=
2
| ||
| 9 |
在Rt△DHF中,DF=
| HF2+DH2 |
31
| ||
| 9 |
∵∠DBF=∠DAB,∠FDB=∠BDA,
∴△DBF∽△DAB,
∴DF:BD=BD:AD,即
31
| ||
| 9 |
| 31 |
| 31 |
∴AD=12
| 3 |
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了勾股定理、相似三角形的判定与性质和含30度的直角三角形三边的关系.

练习册系列答案
相关题目
 如图,四边形ABCD中AB∥CD,对角线AC,BD相交于O,点E,F分别为BD上两点,且BE=DF,∠AEF=∠CFB.
如图,四边形ABCD中AB∥CD,对角线AC,BD相交于O,点E,F分别为BD上两点,且BE=DF,∠AEF=∠CFB. 如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,求△EBG的周长.
如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,求△EBG的周长. 如图,四边形ABCD是一个长方形的台球桌,台球桌上还剩一个黑球没有被打进球袋,在点P的位置,现在轮到你打,你应该把在点Q位置的白球打到AB边上的哪一个点,才能反弹回来撞到黑球?试作图说明.
如图,四边形ABCD是一个长方形的台球桌,台球桌上还剩一个黑球没有被打进球袋,在点P的位置,现在轮到你打,你应该把在点Q位置的白球打到AB边上的哪一个点,才能反弹回来撞到黑球?试作图说明.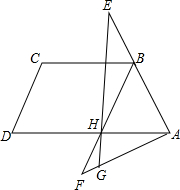 如图,等腰梯形ABCD中,AD∥BC,H是AD中点,AB=BC=CD=
如图,等腰梯形ABCD中,AD∥BC,H是AD中点,AB=BC=CD=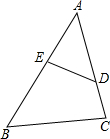 若∠ADE=∠B,AD=6,AB=12,DE=5,则BC的长为
若∠ADE=∠B,AD=6,AB=12,DE=5,则BC的长为