题目内容
已知⊙O的半径为r,圆内接正三角形的边长为a,圆内接正方形的边长为b,则a,b有何确定的等量关系?
考点:正多边形和圆
专题:
分析:首先根据题意画出图形,然后由图形,根据含30°的直角三角形的性质与等腰直角三角形求解即可求得a与b的值,继而求得答案.
解答: 解:如图(1)∵正三角形的中心角∠BOC=
解:如图(1)∵正三角形的中心角∠BOC=
=120°,OB=OC,
∴∠BOD=60°,
∴BD=OB•sin60°,
∴边长a=2BD=2×r×sin60°=
r;
如图(2),∵内接正方形的圆心角∠BOC=90°,OB=OC,
∴正方形的边长b=
r;
∴a,b的等量关系为:
a=
b.
 解:如图(1)∵正三角形的中心角∠BOC=
解:如图(1)∵正三角形的中心角∠BOC=| 360° |
| 3 |
∴∠BOD=60°,
∴BD=OB•sin60°,
∴边长a=2BD=2×r×sin60°=
| 3 |
如图(2),∵内接正方形的圆心角∠BOC=90°,OB=OC,
∴正方形的边长b=
| 2 |
∴a,b的等量关系为:
| 2 |
| 3 |
点评:此题考查了正多边形与圆的知识.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法正确的是( )
| A、任意两个等腰三角形都相似 |
| B、任意两个菱形都相似 |
| C、任意两个正五边形都相似 |
| D、对应角相等的两个多边形相似 |
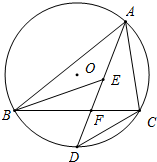 如图,已知△ABC内接于⊙O,AD平分∠BAC交BC于点F,交⊙O于点D,E是△ABC内心,连BE.
如图,已知△ABC内接于⊙O,AD平分∠BAC交BC于点F,交⊙O于点D,E是△ABC内心,连BE.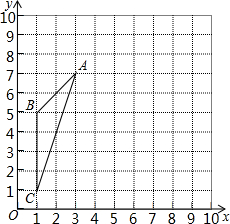 如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.建立如图所示的直角坐标系,
如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.建立如图所示的直角坐标系,


