题目内容
 如图,四边形ABCD中AB∥CD,对角线AC,BD相交于O,点E,F分别为BD上两点,且BE=DF,∠AEF=∠CFB.
如图,四边形ABCD中AB∥CD,对角线AC,BD相交于O,点E,F分别为BD上两点,且BE=DF,∠AEF=∠CFB.(1)求证:四边形ABCD是平行四边形;
(2)若AC=2OE,试判断四边形AECF的形状,并说明理由.
考点:平行四边形的判定,矩形的判定
专题:
分析:(1)证得AB平行且等于CD,利用一组对边平行且相等的四边形是平行四边形进行判断即可;
(2)根据平行四边形的性质证得四边形ACEF为平行四边形,然后利用矩形的判定定理判定该平行四边形为矩形即可.
(2)根据平行四边形的性质证得四边形ACEF为平行四边形,然后利用矩形的判定定理判定该平行四边形为矩形即可.
解答:(1)证明:
∵AB∥CD,
∴∠ABD=∠CDB,
又∵∠AEF=∠CFB,
∴∠AEB=∠CFD,
又∵BE=DF,
∴△ABE≌△CDF(ASA),
∴AB=CD,
又∵AB∥CD,
∴四边形ABCD是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴OB=OD OA=OC=
AC
∵BE=DF
∴OB-BE=DO-DF
∴OE=OF
又∵OA=OC
∴四边形AECF是平行四边形
又∵AC=2OE,EF=2OE
∴AC=EF
∴平行四边形AECF是矩形.
∵AB∥CD,
∴∠ABD=∠CDB,
又∵∠AEF=∠CFB,
∴∠AEB=∠CFD,
又∵BE=DF,
∴△ABE≌△CDF(ASA),
∴AB=CD,
又∵AB∥CD,
∴四边形ABCD是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴OB=OD OA=OC=
| 1 |
| 2 |
∵BE=DF
∴OB-BE=DO-DF
∴OE=OF
又∵OA=OC
∴四边形AECF是平行四边形
又∵AC=2OE,EF=2OE
∴AC=EF
∴平行四边形AECF是矩形.
点评:本题考查了矩形的判定、平行四边形的判定及性质,属于四边形的基础知识,难度不大.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
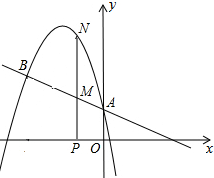 如图,二次函数y=-
如图,二次函数y=-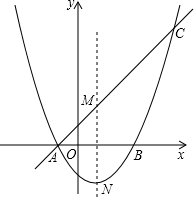 如图,抛物线y=
如图,抛物线y=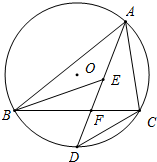 如图,已知△ABC内接于⊙O,AD平分∠BAC交BC于点F,交⊙O于点D,E是△ABC内心,连BE.
如图,已知△ABC内接于⊙O,AD平分∠BAC交BC于点F,交⊙O于点D,E是△ABC内心,连BE.