题目内容
12.先阅读,理解下面例题,再按要求解答例题:解一元二次不等式x2-9>0
解:∵x2-9=(x+3)(x-3)∴(x+3)(x-3)>0
由有理数的乘法法则“两数相乘,同号得正”有①$\left\{{\begin{array}{l}{x+3>0}\\{x-3>0}\end{array}}\right.$或 ②$\left\{{\begin{array}{l}{x+3<0}\\{x-3<0}\end{array}}\right.$
解不等式组①得x>3
解不等式组②得x<-3
故不等式的解集为x>3或x<-3
问题:求分式不等式$\frac{5x+1}{2x-3}<2$的解集.
分析 先根据$\frac{5x+1}{2x-3}<2$得到$\frac{5x+1}{2x-3}$-2<0,进一步得到$\frac{5x+1-2(2x-3)}{2x-3}$<0,再根据除法的法则转化为两个不等式组,解不等式组即可求解.
解答 解:$\frac{5x+1}{2x-3}<2$,
$\frac{5x+1}{2x-3}$-2<0,
$\frac{5x+1-2(2x-3)}{2x-3}$<0,
$\frac{x+7}{2x-3}$<0,
由有理数的乘法法则“两数相乘,异号得负”有①$\left\{\begin{array}{l}{x+7>0}\\{2x-3<0}\end{array}\right.$或②$\left\{\begin{array}{l}{x+7<0}\\{2x-3>0}\end{array}\right.$,
解不等式组①得-7<x<1.5;
解不等式组②得无解.
故不等式的解集为-7<x<1.5.
点评 本题考查了一元二次不等式,不等式组的解法,根据除法法则转化为不等式组的问题是关键.

练习册系列答案
相关题目
20.在△ABC中,AB=AC=4,∠B=30°,点P是线段BC上一动点,则线段AP的长可能是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
4.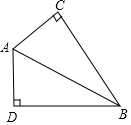 如图,∠C=∠D=90°,AC=AD,那么△ABC与△ABD全等的理由是( )
如图,∠C=∠D=90°,AC=AD,那么△ABC与△ABD全等的理由是( )
 如图,∠C=∠D=90°,AC=AD,那么△ABC与△ABD全等的理由是( )
如图,∠C=∠D=90°,AC=AD,那么△ABC与△ABD全等的理由是( )| A. | HL | B. | SAS | C. | ASA | D. | AAS |
1.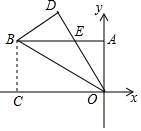 长方形OABC在平面直角坐标系内的位置如图所示,将长方形沿BO折叠,使点C落在点D处,DO与AB交于点E,BC=4cm,BA=8cm,则点E的坐标为( )
长方形OABC在平面直角坐标系内的位置如图所示,将长方形沿BO折叠,使点C落在点D处,DO与AB交于点E,BC=4cm,BA=8cm,则点E的坐标为( )
 长方形OABC在平面直角坐标系内的位置如图所示,将长方形沿BO折叠,使点C落在点D处,DO与AB交于点E,BC=4cm,BA=8cm,则点E的坐标为( )
长方形OABC在平面直角坐标系内的位置如图所示,将长方形沿BO折叠,使点C落在点D处,DO与AB交于点E,BC=4cm,BA=8cm,则点E的坐标为( )| A. | (-3,4) | B. | (-3.5,4) | C. | (-3.7,4) | D. | (-4,4) |
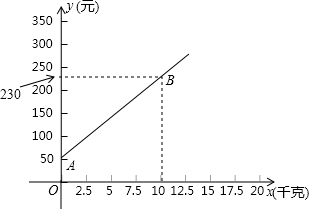 我县甲、乙两家甜橘柚基地生产的甜橘柚品质相同,销售价格也相同.“元旦”期间,两家均推出了优惠方案,甲基地的优惠方案是:每个游客进园需购买门票,采摘的甜橘柚打六折优惠;乙基地的优惠方案是:每个游客进园不需购买门票,采摘园的甜橘柚超过10千克后,超过部分打五折优惠.优惠期间,设某游客的甜橘柚采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中射线AB表示y1与x之间的函数关系.
我县甲、乙两家甜橘柚基地生产的甜橘柚品质相同,销售价格也相同.“元旦”期间,两家均推出了优惠方案,甲基地的优惠方案是:每个游客进园需购买门票,采摘的甜橘柚打六折优惠;乙基地的优惠方案是:每个游客进园不需购买门票,采摘园的甜橘柚超过10千克后,超过部分打五折优惠.优惠期间,设某游客的甜橘柚采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中射线AB表示y1与x之间的函数关系. 如图,甲、乙两楼楼顶上的点A和点E与地面上的点C这三点在同一条直线上,点B、D分别在点E、A的正下方且D、B、C三点在同一条直线上,B、C相距50米,D、C相距80米,乙楼高BE为20米,求甲楼高AD.
如图,甲、乙两楼楼顶上的点A和点E与地面上的点C这三点在同一条直线上,点B、D分别在点E、A的正下方且D、B、C三点在同一条直线上,B、C相距50米,D、C相距80米,乙楼高BE为20米,求甲楼高AD. 已知.
已知.