题目内容
1.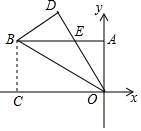 长方形OABC在平面直角坐标系内的位置如图所示,将长方形沿BO折叠,使点C落在点D处,DO与AB交于点E,BC=4cm,BA=8cm,则点E的坐标为( )
长方形OABC在平面直角坐标系内的位置如图所示,将长方形沿BO折叠,使点C落在点D处,DO与AB交于点E,BC=4cm,BA=8cm,则点E的坐标为( )| A. | (-3,4) | B. | (-3.5,4) | C. | (-3.7,4) | D. | (-4,4) |
分析 由矩形的性质得出∠OAB=90°,OA=BC=4cm,AB∥OC,与平行线的性质得出∠EBO=∠BOC,由折叠的性质得:∠EOB=∠BOC,得出∠EBC=∠EOB,证出OE=BE,设AE=x,则OE=BE=8-x,在Rt△OAE中,由勾股定理得出方程,解方程求出AE=3,即可得出点E的坐标.
解答 解:∵四边形OABC是矩形,
∴∠OAB=90°,OA=BC=4cm,AB∥OC,
∴∠EBO=∠BOC,
由折叠的性质得:∠EOB=∠BOC,
∴∠EBC=∠EOB,
∴OE=BE,
设AE=x,则OE=BE=8-x,
在Rt△OAE中,由勾股定理得:AE2+OA2=OE2,
即x2+42=(8-x)2,
解得:x=3,
∴AE=3,
∴点E的坐标为(-3,4);
故选:A.
点评 本题考查了折叠的性质、坐标与图形性质、矩形的性质、等腰三角形的判定、平行线的性质、勾股定理等知识;熟练掌握折叠的性质,证出OE=BE,再由勾股定理得出方程是解决问题的关键.

练习册系列答案
相关题目
13.数轴上的一点M对应的数为-1,点N表示的数比点M表示的数大3,则点N表示的数为( )

| A. | A点 | B. | B点 | C. | C点 | D. | D点 |
10.下列根式中不是最简二次根式的是( )
| A. | $\sqrt{13}$ | B. | $\sqrt{12}$ | C. | $\sqrt{{a}^{2}+4}$ | D. | $\sqrt{2}$ |
11.下列结论正确的是( )
| A. | 近似数1.230和1.23表示的意义相同 | |
| B. | 近似数79.0是精确到个位的数 | |
| C. | 将数60340精确到千位是6.0×104 | |
| D. | 近似数5千与近似数5000的精确度相同 |

 平行四边形ABCD在平面直角坐标系中的位置如图所示,其中A(-6,0),B(4,0),C(5,3),反比例函数y=$\frac{k}{x}$的图象经过点C.
平行四边形ABCD在平面直角坐标系中的位置如图所示,其中A(-6,0),B(4,0),C(5,3),反比例函数y=$\frac{k}{x}$的图象经过点C. 如图,在△ABC和△DEF中,已知AB=DE,BC=EF,根据(SAS)判定△ABC≌△DEF,还需的条件是∠B=∠E.
如图,在△ABC和△DEF中,已知AB=DE,BC=EF,根据(SAS)判定△ABC≌△DEF,还需的条件是∠B=∠E.