先化简.再求值:$\frac{{x}^{2}}{{x}^{2}-2x+1}$÷.其中x=2018．题目和参考答案——青夏教育精英家教网—

题目内容

17．先化简，再求值：$\frac{{x}^{2}}{{x}^{2}-2x+1}$÷（x+1+$\frac{1}{x-1}$），其中x=2018．

分析根据分式的混合运算顺序和法则化简原式，再将x的值代入即可得．

解答解：原式=$\frac{{x}^{2}}{（x-1）^{2}}$÷（$\frac{{x}^{2}-1}{x-1}$+$\frac{1}{x-1}$）
=$\frac{{x}^{2}}{（x-1）^{2}}$•$\frac{x-1}{{x}^{2}}$
=$\frac{1}{x-1}$，
当x=2018时，原式=$\frac{1}{2017}$．

点评本题主要考查分式的化简求值能力，熟练掌握分式的混合运算顺序和法则是解题的关键．

练习册系列答案

8．如图1，在Rt△ABC中，∠ACB=90°，BC＞AC，矩形CDEF的顶点D是线段BC上一动点，点F在射线CA上，且CF=2CD，点D从点C出发，运动至点B停止，设CF=x，矩形CDEF与△ABC重合部分的面积为y，y关于x的函数图象如图2所示（其中0＜x≤m，m＜x≤4，4＜x≤16时，函数的关系式不同）．
（1）填空：BC的长为8；
（2）求y关于x的函数关系式，并写出x的取值范围．

5．某地计划用80-120天（含80与120天）的时间建设一项水利工程，工程需要运送的土石方总量为360万米³．
（1）写出运输公司完成任务所需的时间y（单位：天）与平均每天的工作量x（单位：万米³）之间的函数关系式，并给出自变量x的取值范围；
（2）由于工程进度的需要，实际运送土石方总量比原计划多400000米³，工期比原计划多用了10天，则平均每天运送土石方数是多少万米³？

12．先阅读，理解下面例题，再按要求解答
例题：解一元二次不等式x²-9＞0
解：∵x²-9=（x+3）（x-3）∴（x+3）（x-3）＞0
由有理数的乘法法则“两数相乘，同号得正”有①$\left\{{\begin{array}{l}{x+3＞0}\\{x-3＞0}\end{array}}\right.$或 ②$\left\{{\begin{array}{l}{x+3＜0}\\{x-3＜0}\end{array}}\right.$
解不等式组①得x＞3
解不等式组②得x＜-3
故不等式的解集为x＞3或x＜-3
问题：求分式不等式$\frac{5x+1}{2x-3}＜2$的解集．

2．解方程
（1）2（3x+4）-5（x+1）=3
（2）$\frac{2x+1}{3}$-$\frac{5x-1}{6}$=1．

9．已知：如图①，在Rt△ABC中，AB⊥AC，AB=3cm，BC=5cm，将△ABC绕AC中点旋转180°得△CDA，如图②，再将△CDA沿AC的方向以1cm/s的速度平移得到△NDP；同时，点Q从点C出发，沿CB方向以1cm/s的速度运动，当△NDP停止平移时，点Q也停止运动，设运动时间为t（s）（0＜t＜4）．解答下列问题．

（1）当t为何值时，PQ∥AB？
（2）设△PQC的面积为y（cm²），求y与t之间的函数关系式；
（3）是否存在某一时刻t，使S_△QDC：S_{四边形ABQP}=1：4？若存在，求出t的值；若不存在，请说明理由．
（4）是否存在某一时刻t，使PQ⊥DQ？若存在，请直接写出t的值；若不存在，请说明理由．

6．

如图，在△ABC和△DEF中，已知AB=DE，BC=EF，根据（SAS）判定△ABC≌△DEF，还需的条件是∠B=∠E．

7．

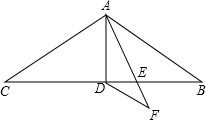如图，在△ABC中，AB=AC=11，∠BAC=120°，AD是△ABC的中线，AE是∠BAD的角平分线，DF∥AB交AE的延长线于点F，则DF的长为（　　）

试题分类