题目内容
1．
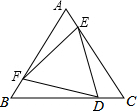如图，在等边△ABC中，AF=BD=CE，求证：△DEF也是等边三角形．
分析 根据等边的性质，以及三角形的判定定理证得△AEF≌△BFD≌△CDE即可得出：△DEF是等边三角形．
解答 证明：∵△ABC为等边三角形，
∴∠A=∠B=∠C=60°，AB=BC
又∵AF=BD
∴BF=CD，
∴在△BFD和△CDE中，
$\left\{\begin{array}{l}{BF=CD}\\{∠B=∠C}\\{BD=CE}\end{array}\right.$，
∴△BFD≌△CDE，
∴BF=DE，
同理DE=DF，
∴DF=DE=EF，即△DEF是等边三角形．
点评 此题主要考查了等边三角形的判定与性质和全等三角形判定，根据已知得出△AEF≌△BFD≌△CDE是解题关键．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
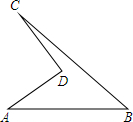实验中学有一块四边形的空地ABCD，如图所示，学校计划在空地上种植草皮，经测量AD=8米，CD=6米，∠ADC=90°，AB=26米，BC=24米，若每平方米草皮需要300元，学校需要投入多少资金买草皮？
9．从正方形的铁皮上，截去2cm宽的一条长方形，余下的长方形面积是48cm2，则原来的正方形铁皮的面积是（ ）
| A． | 68cm2 | B． | 64cm2 | C． | 9cm2 | D． | 8cm2 |
如图，已知AB=CD，∠A=∠D，∠E=∠F．若EC=6，则BF=6．
如图，D为线段BC的中点，过点D作AD⊥BC，点E在AD上，连结AB、AC、EB、EC，求证：∠ABE=∠ACE．