题目内容
11.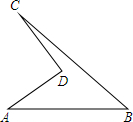 实验中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,若每平方米草皮需要300元,学校需要投入多少资金买草皮?
实验中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,若每平方米草皮需要300元,学校需要投入多少资金买草皮?
分析 连接AC,根据勾股定理求出AC,根据勾股定理的逆定理求出∠ACB=90°,求出区域的面积,即可求出答案.
解答 解:连结AC, 如图所示:
如图所示:
在Rt△ACD中,∠ADC=90°,AD=4米,CD=3米,
由勾股定理得:AC=$\sqrt{{8}^{2}+{6}^{2}}$=10(米),
∵AC2+BC2=102+242=676,AB2=262=676,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴该区域面积S=S△ACB-S△ADC=$\frac{1}{2}$×10×24-$\frac{1}{2}$×6×8=96(平方米),
96×300=28800(元).
∴学校需要投入28800元资金买草皮.
点评 本题考查了勾股定理,三角形面积,勾股定理的逆定理的应用;解此题的关键是求出区域的面积.

练习册系列答案
相关题目
2.下面对关于x的一元二次方程a(x-1)2=2x2-2的表述错误的是( )
| A. | 判别式的值为16 | B. | 方程有一根是1 | C. | a不等于0 | D. | a不等于2 |
 已知,如图,在△ABC中,AB=AC,∠ABC=∠ACB,D是AB的中点,DE⊥AB交AC于E,若∠BEC=∠C.
已知,如图,在△ABC中,AB=AC,∠ABC=∠ACB,D是AB的中点,DE⊥AB交AC于E,若∠BEC=∠C.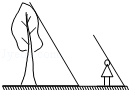 某数学兴趣小组利用太阳光测量一棵树的高度(如图),在同一时刻,测得树的影长为4.8米,小明的影长为1.2米,已知小明的身高为1.5米,则树高为6米.
某数学兴趣小组利用太阳光测量一棵树的高度(如图),在同一时刻,测得树的影长为4.8米,小明的影长为1.2米,已知小明的身高为1.5米,则树高为6米.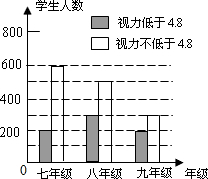 某学习小组对所在城区初中学生的视力情况进行抽样调查,如图是这些同学根据调查结果画出的条形统计图,请根据图中信息解决下列问题:
某学习小组对所在城区初中学生的视力情况进行抽样调查,如图是这些同学根据调查结果画出的条形统计图,请根据图中信息解决下列问题: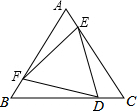 如图,在等边△ABC中,AF=BD=CE,求证:△DEF也是等边三角形.
如图,在等边△ABC中,AF=BD=CE,求证:△DEF也是等边三角形.