题目内容
8.(1)尝试计算:m1=2×3=$\frac{1}{a}$(2×3×4-1×2×3);m2=3×4=$\frac{1}{a}$(3×4×5-b×3×4);m3=4×5=$\frac{1}{a}$(4×5×c-3×4×5);…直接写出等式中a、b、c的值
(2)规律提炼:写出第n个等式(用含有字母n的式子表示)
(3)问题解决:求m1+m2+m3+…+m99的值.
分析 (1)根据代数式的运算,找出关于a、b、c的一元一次方程,解方程即可得出结论;
(2)根据给定的m1、m2、m3的值,找出变化规律“mn=(n+1)(n+2)=$\frac{1}{3}$×[(n+1)(n+2)(n+3)-n(n+1)(n+2)]”,此题得解;
(3)代入mn的值,即可得出结论.
解答 解:(1)∵m1=2×3=$\frac{1}{a}$(2×3×4-1×2×3)=$\frac{1}{a}$×(4-1)×2×3,
∴a=3;
∵m2=3×4=$\frac{1}{a}$(3×4×5-b×3×4)=$\frac{1}{3}$×(5-b)×3×4,
∴b=2;
∵m3=4×5=$\frac{1}{a}$(4×5×c-3×4×5)=$\frac{1}{3}$×(c-3)×4×5,
∴c=6.
(2)观察,发现规律:m1=2×3=$\frac{1}{3}$×(2×3×4-1×2×3),m2=3×4=$\frac{1}{3}$×(3×4×5-2×3×4),m3=4×5=$\frac{1}{3}$×(4×5×6-3×4×5),…,
∴mn=(n+1)(n+2)=$\frac{1}{3}$×[(n+1)(n+2)(n+3)-n(n+1)(n+2)].
(3)m1+m2+m3+…+m99=$\frac{1}{3}$×2×3×4-$\frac{1}{3}$×1×2×3+$\frac{1}{3}$×3×4×5-$\frac{1}{3}$×2×3×4+$\frac{1}{3}$×4×5×6-$\frac{1}{3}$×3×4×5+…+$\frac{1}{3}$×100×101×102-$\frac{1}{3}$×99×100×101=$\frac{1}{3}$×100×101×102-$\frac{1}{3}$×1×2×3=343998.
点评 本题考查了规律型中数字的变化类,根据给定的算式的变化找出变化规律是解题的关键.

| A. |  | B. |  | C. |  | D. |  |
| A. | 0或8 | B. | 0 | C. | 8 | D. | 2 |
| A. | 3<a<5 | B. | -5<a<3 | C. | -5<a<-3 | D. | 不能确定 |
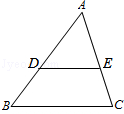 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,$\frac{AD}{BD}$=$\frac{3}{4}$,求CE的长.
如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,$\frac{AD}{BD}$=$\frac{3}{4}$,求CE的长.