题目内容

17．一元二次方程x2-mx+2m=0有两个相等的实数根，则m等于（　　）
A．0或8B．0C．8D．2

分析 根据方程有两个相等实数根可得△=（-m）2-4×1×2m=0，解之即可．

解答 解：根据题意知，△=（-m）2-4×1×2m=0，
即m2-8m=0，
解得：m=0或m=8，
故选：A．

点评 本题主要考查根的判别式，一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：
①当△＞0时，方程有两个不相等的两个实数根，②当△=0时，方程有两个相等的两个实数根；③当△＜0时，方程无实数根．

练习册系列答案
相关题目
7．已知|a|=3，|b|=5，
①若a•b＜0，求a-b的值；
②若|a+b|=-（a+b），求a-b的值．
8．（1）尝试计算：m1=2×3=$\frac{1}{a}$（2×3×4-1×2×3）；m2=3×4=$\frac{1}{a}$（3×4×5-b×3×4）；m3=4×5=$\frac{1}{a}$（4×5×c-3×4×5）；…
直接写出等式中a、b、c的值
（2）规律提炼：写出第n个等式（用含有字母n的式子表示）
（3）问题解决：求m1+m2+m3+…+m99的值．
5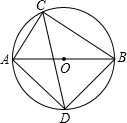．如图，圆O的直径AB为4，点C在圆O上，∠ACB的平分线交圆O于点D，连接AD、BD，则AD的长等于（　　）
A．2B．3C．2$\sqrt{2}$D．2$\sqrt{3}$
12．已知函数y=-（x-1）2+4．
（1）当x=1时，抛物线有最大值，是4．
（2）当x＜1 时，y随x的增大而增大；
（3）该函数图象可由y=-x2的图象经过怎样的平移得到？
（4）求出该抛物线与x轴的交点坐标；
（5）求出该抛物线与y轴的交点坐标．
2．下列运算错误的是（　　）
A．3a•（-2a）2=12a3B．3x4-x4=2x4C．xy4÷（-xy）=-xy3D．-（2x3y2）3=-8x9y6
9．为拉动内需促进消费，某品牌的电视机经过两次降价，从原来每台6000元降到现在的每台4860元，求平均每次的降价率是多少？设每次降价率为x，由题意列方程为（　　）
A．4860（1+x）2=6000B．4860（1-x）2=6000C．6000（1-x）2=4860D．6000（1+x）2=4860
6．化简（2a-3b）-3（4a-2b）结果为（　　）
A．-10a-3bB．-10a+3bC．10a-9bD．10a+9b
7．给出下列命题：
①在直角三角形ABC中，已知两边长为3和4，则第三边长为5；
②三角形的三边a、b、c满足a2+c2=b2，则∠C=90°；
③△ABC中，若∠A：∠B：∠C=1：5：6，则△ABC是直角三角形；
④△ABC中，若三边长分别为3a、4a、5a（a＞0），则这个三角形是直角三角形．
其中，假命题的个数为（　　）
A．1个B．2个C．3个D．4个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网