题目内容
16.若直角三角形的三边分别为3,4,x,则x2=25或7.分析 本题已知直角三角形的两边长,但未明确这两条边是直角边还是斜边,因此两条边中的较长边4既可以是直角边,也可以是斜边,所以求第三边的长必须分类讨论,即4是斜边或直角边的两种情况,然后利用勾股定理求解.
解答 解:设第三边为x,
(1)若4是直角边,则第三边x是斜边,由勾股定理得:
32+42=x2,所以x2=25;
(2)若4是斜边,则第三边x为直角边,由勾股定理得:
32+x2=42,所以x2=7;
故答案为25或7;
点评 本题考查了利用勾股定理解直角三角形的能力,当已知条件中没有明确哪是斜边时,要注意讨论,一些学生往往忽略这一点,造成丢解.

练习册系列答案
相关题目
4. 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )
 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
5.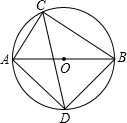 如图,圆O的直径AB为4,点C在圆O上,∠ACB的平分线交圆O于点D,连接AD、BD,则AD的长等于( )
如图,圆O的直径AB为4,点C在圆O上,∠ACB的平分线交圆O于点D,连接AD、BD,则AD的长等于( )
 如图,圆O的直径AB为4,点C在圆O上,∠ACB的平分线交圆O于点D,连接AD、BD,则AD的长等于( )
如图,圆O的直径AB为4,点C在圆O上,∠ACB的平分线交圆O于点D,连接AD、BD,则AD的长等于( )| A. | 2 | B. | 3 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
6.化简(2a-3b)-3(4a-2b)结果为( )
| A. | -10a-3b | B. | -10a+3b | C. | 10a-9b | D. | 10a+9b |
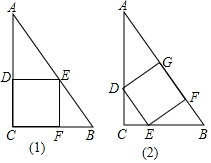 已知直角三角形的铁片ABC的两条直角边BC、AC的长分别为3、4,按图示所采用两种方法,各剪一块正方形的铁片,试比较哪一种方法剪出的正方形的面积较大.
已知直角三角形的铁片ABC的两条直角边BC、AC的长分别为3、4,按图示所采用两种方法,各剪一块正方形的铁片,试比较哪一种方法剪出的正方形的面积较大.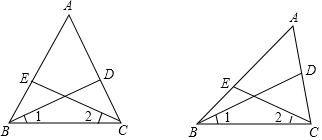
 如图:正方形ABCD中,点E在AB上,点F在BC的延长线上,且AE=CF,DG⊥EF于H交BC于G.若tan∠BHG=$\frac{3}{4}$,△BGH的面积为3,求DK的长为5.
如图:正方形ABCD中,点E在AB上,点F在BC的延长线上,且AE=CF,DG⊥EF于H交BC于G.若tan∠BHG=$\frac{3}{4}$,△BGH的面积为3,求DK的长为5.