题目内容
14.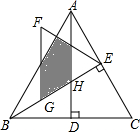 如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4$\sqrt{3}$,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{5\sqrt{3}}{2}$.
如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4$\sqrt{3}$,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{5\sqrt{3}}{2}$.
分析 根据等边三角形的性质,可得AD的长,∠ABG=∠HBD=30°,根据等边三角形的判定,可得△MEH的形状,根据直角三角形的判定,可得△FIN的形状,根据面积的和差,可得答案.
解答 解:如图所示: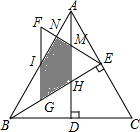 ,
,
由△ABC是等边三角形,高AD、BE相交于点H,BC=4$\sqrt{3}$,得
AD=BE=$\frac{\sqrt{3}}{2}$BC=6,∠ABG=∠HBD=30°.
由直角三角的性质,得∠BHD=90°-∠HBD=60°.
由对顶角相等,得∠MHE=∠BHD=60°
由BG=2,得EG=BE-BG=6-2=4.
由GE为边作等边三角形GEF,得
FG=EG=4,∠EGF=∠GEF=60°,
△MHE是等边三角形;
S△ABC=$\frac{1}{2}$AC•BE=$\frac{1}{2}$AC×EH×3
EH=$\frac{1}{3}$BE=$\frac{1}{3}$×6=2.
由三角形外角的性质,得∠BIG=∠FGE-∠IBG=60°-30°=30°,
由∠IBG=∠BIG=30°,得IG=BG=2,
由线段的和差,得IF=FG-IG=4-2=2,
由对顶角相等,得∠FIN=∠BIG=30°,
由∠FIN+∠F=90°,得∠FNI=90°,
由锐角三角函数,得FN=1,IN=$\sqrt{3}$.
S五边形NIGHM=S△EFG-S△EMH-S△FIN
=$\frac{\sqrt{3}}{4}$×42-$\frac{\sqrt{3}}{4}$×22-$\frac{1}{2}$×$\sqrt{3}$×1=$\frac{5\sqrt{3}}{2}$,
故答案为:$\frac{5\sqrt{3}}{2}$.
点评 本题考查了等边三角形的判定与性质,利用了等边三角形的判定与性质,直角三角形的判定,利用图形的割补法是求面积的关键.

| A. | (x-2)2=3 | B. | (x+2)2-3=0 | C. | (x-2)2=0 | D. | x(x-4)=-1 |
| 第1行 | 1 2 3 |
| 第2行 | 4 5 6 7 8 |
| 第3行 | 9 10 11 12 13 14 15 |
| 第4行 | 16 17 18 19 20 21 22 23 24 |
| … | … |
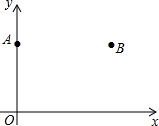 如图,在平面直角坐标系xOy中,点A(0,3),点B(4,3).
如图,在平面直角坐标系xOy中,点A(0,3),点B(4,3).
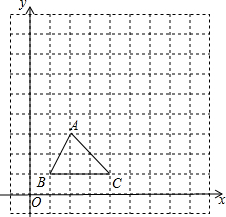 如图,在边长为1个单位长度的小正方形网格中:
如图,在边长为1个单位长度的小正方形网格中: 已知,如图,AB=CD,∠PAB的面积等于△PCD的面积,求证:OP平分∠BOD.
已知,如图,AB=CD,∠PAB的面积等于△PCD的面积,求证:OP平分∠BOD.