题目内容
12.某商店进行促销活动,如果将进价为8元/件的商品按每件10元出售,每天可销售100件,现采用提高售价,减少进货量的办法增加利润,已知这种商品的单价每涨1元,其销售量就要减少10件,问将售价定为多少元/件时,才能使每天所赚的利润最大?并求出最大利润.分析 确定每件利润、销售量,根据利润=每件利润×销售量,得出销售利润y(元)与销售单价x(元)之间的函数关系,利用配方法确定函数的最值.
解答 解:设销售价每件定为x元,则每件利润为(x-8)元,销售量为[100-10(x-10)],
根据利润=每件利润×销售量,
可得销售利润y=(x-8)•[100-10(x-10)]=-10x2+280x-1600=-10(x-14)2+360,
∴当x=14时,y的最大值为360元,
∴应把销售价格定为每件14元,可使每天销售该商品所赚利润最大,最大利润为360元.
点评 此题考查二次函数的性质及其应用,将实际问题转化为求函数最值问题,从而来解决实际问题,比较简单.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.分式方程$\frac{2-m}{x-1}$=$\frac{1}{x}$无解,则m的值为( )
| A. | 2 | B. | 1 | C. | 1或2 | D. | 0或2 |
7.已知抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,其中A(-1,0)点D是抛物线y=$\frac{1}{2}$x2+bx-2的顶点,点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,m的值是( )
| A. | $\frac{25}{40}$ | B. | $\frac{24}{41}$ | C. | $\frac{23}{40}$ | D. | $\frac{25}{41}$ |
4.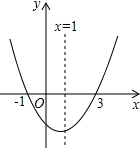 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②b+2a=0;③x=3是关于x的方程ax2+bx+c=0(a≠0)的一个根;④a+c>b;⑤3a+c=0.其中正确的结论有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②b+2a=0;③x=3是关于x的方程ax2+bx+c=0(a≠0)的一个根;④a+c>b;⑤3a+c=0.其中正确的结论有( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②b+2a=0;③x=3是关于x的方程ax2+bx+c=0(a≠0)的一个根;④a+c>b;⑤3a+c=0.其中正确的结论有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②b+2a=0;③x=3是关于x的方程ax2+bx+c=0(a≠0)的一个根;④a+c>b;⑤3a+c=0.其中正确的结论有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
1.菱形的边长是10,一条对角线长是12,则此菱形的另一条对角线是( )
| A. | 10 | B. | 24 | C. | 8 | D. | 16 |
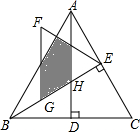 如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4$\sqrt{3}$,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{5\sqrt{3}}{2}$.
如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4$\sqrt{3}$,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{5\sqrt{3}}{2}$. 如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A、C两点,与x轴的另一交点为点B.
如图,在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=-$\frac{3}{2}$且经过A、C两点,与x轴的另一交点为点B.