题目内容
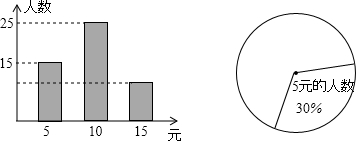
9.如图是我市某校八年级学生为贫困山区学生捐款情况抽样调查的条形图和扇形统计图.(1)求本次抽样的学生有多少人;
(2)在扇形统计图中,求该样本中捐款15元的人数所占的圆心角度数;
(3)若该校八年级学生有800人,据此样本求八年级捐款总数.
分析 (1)用捐款5元的人数除以它所占的百分比即可解答;
(2)用样本容量分别减去捐款5元的人数和捐款10元的人数得到捐款15元的人数,于是可计算出捐款15元的人数的百分比,然后用360°乘以这个百分比即可得到捐款15元的人数所占的圆心角的度数;
(3)先样本的平均数,根据样本估计总体,用800乘以这个平均数可估计出九年级学生捐款总数.
解答 解:(1)15÷30%=50(人),
答:本次抽样的学生有50人;
(2)捐款15元的人数=50-15-25=10(人),
360°×$\frac{10}{50}$=72°,
答:该样本中捐款15元的人数所占的圆心角度数为72°;
(3)据此信息可估计该校六年级学生每人捐款为:
(5×15+10×25+15×10)÷(15+25+10)
=720÷50
=9.5(元)
9.5×800=7600(元).
答:八年级捐款总数为7600元.
点评 本题考查了条形统计图:条形统计图是用线段长度表示数据,根据数量的多少画成长短不同的矩形直条,然后按顺序把这些直条排列起来.从条形图可以很容易看出数据的大小,便于比较.也考查了样本估计总体和扇形统计图.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
19.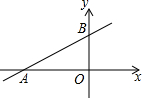 如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,1)两点,则不等式-kx-b<0的解集为( )
如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,1)两点,则不等式-kx-b<0的解集为( )
 如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,1)两点,则不等式-kx-b<0的解集为( )
如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,1)两点,则不等式-kx-b<0的解集为( )| A. | x>-3 | B. | x<-3 | C. | x>3 | D. | x<3 |
20.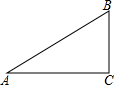 如图在Rt△ABC中,∠C=90°,AB=15,sinA=$\frac{1}{3}$,则BC等于( )
如图在Rt△ABC中,∠C=90°,AB=15,sinA=$\frac{1}{3}$,则BC等于( )
 如图在Rt△ABC中,∠C=90°,AB=15,sinA=$\frac{1}{3}$,则BC等于( )
如图在Rt△ABC中,∠C=90°,AB=15,sinA=$\frac{1}{3}$,则BC等于( )| A. | 45 | B. | 5 | C. | $\frac{1}{5}$ | D. | $\frac{1}{45}$ |
7.已知抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,其中A(-1,0)点D是抛物线y=$\frac{1}{2}$x2+bx-2的顶点,点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,m的值是( )
| A. | $\frac{25}{40}$ | B. | $\frac{24}{41}$ | C. | $\frac{23}{40}$ | D. | $\frac{25}{41}$ |
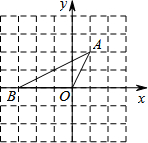 如图,把直角坐标系xOy放置在边长为1的正方形网格中,O是坐标原点,点A、O、B均在格点上,将△OAB绕O点按顺时针方向旋转90°后,得到△OA′B′.
如图,把直角坐标系xOy放置在边长为1的正方形网格中,O是坐标原点,点A、O、B均在格点上,将△OAB绕O点按顺时针方向旋转90°后,得到△OA′B′.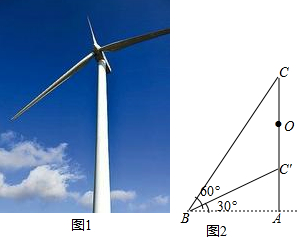
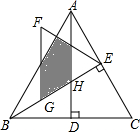 如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4$\sqrt{3}$,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{5\sqrt{3}}{2}$.
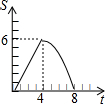
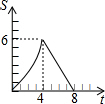
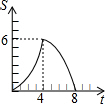
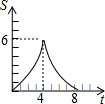
如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4$\sqrt{3}$,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{5\sqrt{3}}{2}$.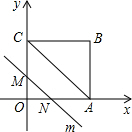 在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒).设△OMN的面积为S,那么能反映S与t之间函数关系的大致图象是( )
在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒).设△OMN的面积为S,那么能反映S与t之间函数关系的大致图象是( )