题目内容
4.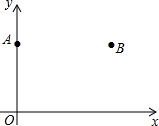 如图,在平面直角坐标系xOy中,点A(0,3),点B(4,3).
如图,在平面直角坐标系xOy中,点A(0,3),点B(4,3).(1)只用直尺(没有刻度)和圆规,求作一点P,使点P同时满足下列两个条件(要求
保留作图痕迹,不必写出作法):
①P到A、B两点的距离相等;
②点P到∠xOy的两边距离相等.
(2)在(1)作出点P后,写出点P的坐标.
分析 (1)作AB的中垂线;再作∠xOy的角平分线,两线的交点就是P点的位置;
(2)根据线段垂直平分线的性质可得P点横坐标为2,再根据角平分线的性质可得点P的坐标为(2,2).
解答  解:(1)作图;
解:(1)作图;
(2)∵点A(0,3),点B(4,3),
∴AB=4,
∵QP是AB的中垂线,
∴P点横坐标为2,
∵P在∠xOy的角平分线上,
∴点P的坐标为(2,2).
点评 此题主要考查了复杂作图,以及角平分线和线段垂直平分线的定义和作法,关键是掌握角的平分线上的点到角的两边的距离相等;经过某一条线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线.

练习册系列答案
相关题目
19.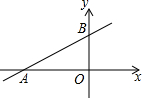 如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,1)两点,则不等式-kx-b<0的解集为( )
如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,1)两点,则不等式-kx-b<0的解集为( )
 如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,1)两点,则不等式-kx-b<0的解集为( )
如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,1)两点,则不等式-kx-b<0的解集为( )| A. | x>-3 | B. | x<-3 | C. | x>3 | D. | x<3 |
9.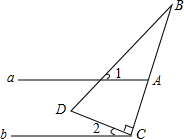 如图,直线a∥b,Rt△BCD如图放置,∠DCB=90°.若∠1+∠B=70°,则∠2的度数为( )
如图,直线a∥b,Rt△BCD如图放置,∠DCB=90°.若∠1+∠B=70°,则∠2的度数为( )
 如图,直线a∥b,Rt△BCD如图放置,∠DCB=90°.若∠1+∠B=70°,则∠2的度数为( )
如图,直线a∥b,Rt△BCD如图放置,∠DCB=90°.若∠1+∠B=70°,则∠2的度数为( )| A. | 20° | B. | 40° | C. | 30° | D. | 25° |
13.分式方程$\frac{2-m}{x-1}$=$\frac{1}{x}$无解,则m的值为( )
| A. | 2 | B. | 1 | C. | 1或2 | D. | 0或2 |
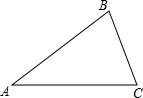 已知:在△ABC中,AB=AC.
已知:在△ABC中,AB=AC.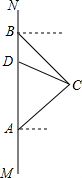 如图,在南北方向的海岸线MN上,有A、B两艘巡船,现均收到故障船C的求救信号.已知A.B两船相距100($\sqrt{3}$+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.已知距观测点D处100海里范围内有暗礁,若巡逻船A沿直线AC去营救船C,在去营救的途中有无触暗礁危险?(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,在南北方向的海岸线MN上,有A、B两艘巡船,现均收到故障船C的求救信号.已知A.B两船相距100($\sqrt{3}$+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.已知距观测点D处100海里范围内有暗礁,若巡逻船A沿直线AC去营救船C,在去营救的途中有无触暗礁危险?(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)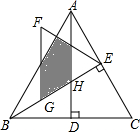 如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4$\sqrt{3}$,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{5\sqrt{3}}{2}$.
如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4$\sqrt{3}$,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为$\frac{5\sqrt{3}}{2}$.